В задаче 1 про скорость прямолинейного движения было получено, что 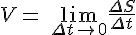 . Это равенство можно записать в виде
. Это равенство можно записать в виде 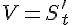 , то есть скорость прямолинейного движения материальной точки в момент времени
, то есть скорость прямолинейного движения материальной точки в момент времени 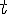 есть производная от пути
есть производная от пути 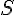 по времени
по времени 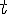 . В этом заключается механический смысл производной.
. В этом заключается механический смысл производной.
Физический смысл производной состоит в следующем. Если функция  описывает какой-либо физический процесс, то производная
описывает какой-либо физический процесс, то производная 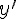 есть скорость протекания этого процесса.
есть скорость протекания этого процесса.
Рассмотрим также геометрический смысл производной. В задаче о касательной к кривой был найден угловой коэффициент касательной 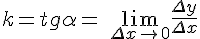 . Это равенство можно записать в виде
. Это равенство можно записать в виде 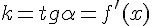 , то есть производная
, то есть производная 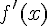 в точке
в точке 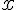 равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции  в точке, абсцисса которой равна
в точке, абсцисса которой равна 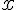 . В этом заключается геометрический смысл производной.
. В этом заключается геометрический смысл производной.
Если точка касания имеет координаты 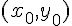 , то угловой коэффициент касательной есть
, то угловой коэффициент касательной есть 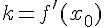 . Например, если касательная к некоторой кривой имеет вид
. Например, если касательная к некоторой кривой имеет вид 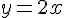 , то производная в точке касания равна 2.
, то производная в точке касания равна 2.
Пользуясь уравнением прямой, проходящей через заданную точку в заданном направлении 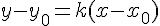 , можно записать уравнение касательной к графику функции
, можно записать уравнение касательной к графику функции  в точке касания
в точке касания 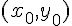 :
:
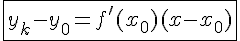 , где
, где 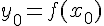 .
.
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой. Так как нормаль перпендикулярна касательной, то её угловой коэффициент равен: 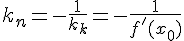 . Поэтому уравнение нормали имеет вид:
. Поэтому уравнение нормали имеет вид:
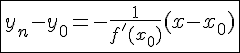 , если
, если 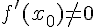
Вопрос. Уравнение касательной к графику некоторой функции в точке 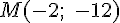 имеет вид
имеет вид 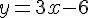 . Найдите значение производной этой функции в точке
. Найдите значение производной этой функции в точке 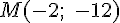 .
.
Начало формы
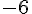 | |
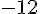 | |
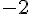 | |
|
 2015-07-14
2015-07-14 5641
5641