Производные константы и произведения константы на функцию

Теорема. Производная константы равна нулю. То есть, если 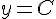, где 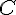константа, то .

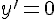Доказательство. Если 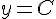, то 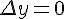. Следовательно, .

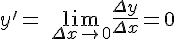Теорема. Константу можно выносить за знак производной.

То есть, если 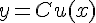, то .

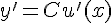Производная суммы, разности, произведения и частного двух функций.

Теорема. Если функци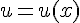и и 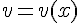дифференцируемы в точке 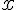, то сумма, разность, произведение и частное этих функций (частное при условии, что 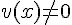) также дифференцируемы в этой точке и имеют место следующие формулы:

1. ;

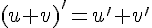2. ;

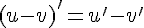3. ;

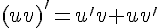4. .

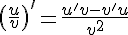Пример. Вычислить производную функции .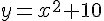

Производная функции 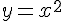равна 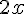, производная константы равна нулю, производная суммы функций равна сумме их производных, следовательно:

.

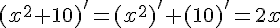Вопрос. Производная функции 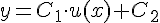равна:

Начало формы

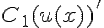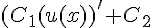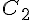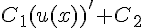Таблица производных элементарных функций

Используя определение, можно найти производные основных элементарных функций, таблица которых представлена ниже:

1. .

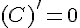2.

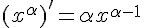
3.

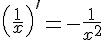
4.

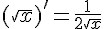
5.

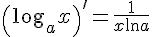
6.

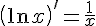
7.

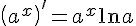
8.

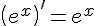
9.

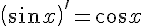
10.

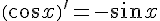
11.

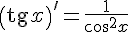
12.

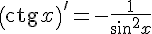
13.

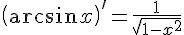
14.

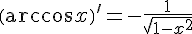
15.

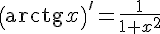
16.

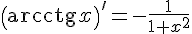
17.

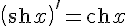
18.

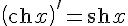
Таблица производных вместе с правилами дифференцирования суммы, разности, произведения, частного, а

также правилом дифференцирования сложной функции составляет основу дифференциального исчисления. Надо отметить также, что производная любой элементарной функции также является элементарной функцией.

Пример. Вычислить производную функции .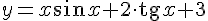
Решение.

Пользуясь правилами дифференцирования суммы, произведения, константы и константы, умноженной на функцию, получаем: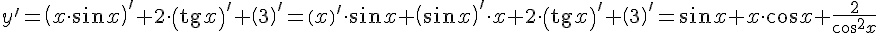

Вопрос. Производная функции 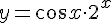равна:

Начало формы

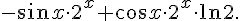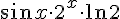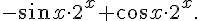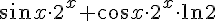Конец формы