Рассмотрим сложную функцию 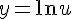 , где
, где 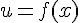 . Найдем производную этой функции по переменной
. Найдем производную этой функции по переменной 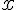 .
.
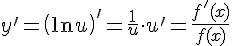 .
.
Или 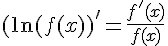 .
.
Производная функции 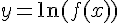 называется логарифмической производной функции
называется логарифмической производной функции  . Логарифмическая производная применяется при вычислении производных показательно-степенных функций.
. Логарифмическая производная применяется при вычислении производных показательно-степенных функций.
Определение. Показательно-степенной функцией называется функция вида 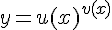 , где
, где 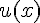 и
и 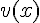 – функции от переменной
– функции от переменной 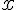 .
.
Примеры показательно-степенных функций: 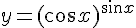 ,
, 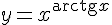 ,
, 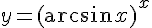 .
.
Найдем производную показательно-степенной функции 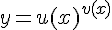 . Предварительно прологарифмируем правую и левую части уравнения.
. Предварительно прологарифмируем правую и левую части уравнения.
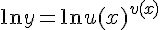 .
.
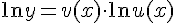
(при этом использовали свойство логарифмов 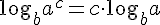 )
)
Дифференцируем обе части по переменной 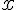 , при этом считаем функцию
, при этом считаем функцию 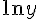 сложной функцией:
сложной функцией:
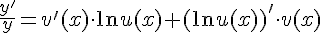 ,
,
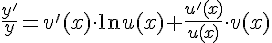 .
.
Выражаем 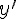 и, учитывая, что
и, учитывая, что 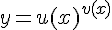 , получаем формулу для вычисления производной показательно-степенной функции:
, получаем формулу для вычисления производной показательно-степенной функции:
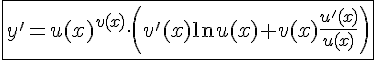 .
.
Пример. Вычислить производную показательно-степенной функции 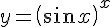 .
.
 2015-07-14
2015-07-14 817
817








