Пусть функция 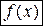 определена в некоторой окрестности точки
определена в некоторой окрестности точки 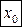 . Точка
. Точка 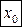 называется точкой максимума (соответственно точкой минимума), если существует такое число
называется точкой максимума (соответственно точкой минимума), если существует такое число 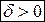 , что для всех
, что для всех 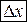 , удовлетворяющих условию
, удовлетворяющих условию 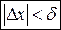 , выполняется неравенство:
, выполняется неравенство:
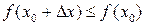 ,
,
(соответственно 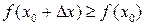 ).
).
Если 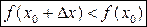 (соответственно
(соответственно  ), то точка
), то точка 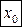 называется точкой строгого максимума (строгого минимума).
называется точкой строгого максимума (строгого минимума).
Точки максимума и минимума называются точками экстремума функции 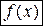 .
.
Теорема (необходимые условия экстремума).
Пусть 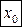 - точка экстремума функции
- точка экстремума функции 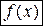 , определенной в некоторой окрестности точки
, определенной в некоторой окрестности точки 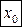 . Тогда либо производная
. Тогда либо производная 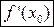 не существует, либо
не существует, либо 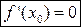 .
.
 2015-07-14
2015-07-14 233
233








