Определение

Функция 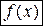называется выпуклой вверх (выпуклой вниз) на интервале 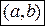. Если для любых трех точек 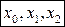, удовлетворяющих неравенству 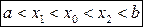, выполняется неравенство:

,

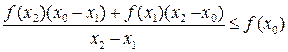(соответственно

).

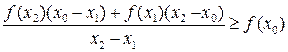Геометрически это означает, что любая точка отрезка, соединяющего точки с координатам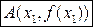и и 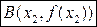, расположена не выше (соответственно не ниже) точки графика функции 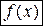, соответствующей тому же значению аргумента.

Теорема (достаточное условие строгой выпуклости).

Пусть функция 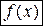дважды дифференцируема на интервале 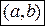. Если 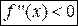на интервале 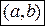, то функция 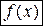строго выпукла вверх на этом интервале. Если 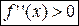на интервале 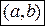, то функция 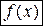строго выпукла вниз на этом интервале.