С помощью производной можно определить сколько решений имеет уравнение. Основную роль здесь играют исследование функций на монотонность, нахождение её экстремальных значений. Кроме того, используется свойство монотонных функций:
Задача 1. Если функция 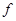 возрастает или убывает на некотором промежутке, то на этом промежутке уравнение
возрастает или убывает на некотором промежутке, то на этом промежутке уравнение 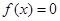 имеет не более одного корня.
имеет не более одного корня.
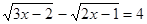 (1)
(1)
Решение: Область определения данного уравнения - промежуток 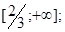 определение на этом промежутке функцию
определение на этом промежутке функцию 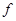 , положив
, положив
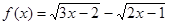
Тогда, на 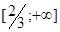
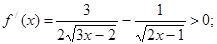
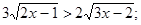
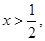
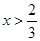 Þ
Þ 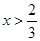 ,
,
и таким образом функция 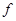 - возрастающая, так что данное уравнение (1) не может иметь более одного решения.
- возрастающая, так что данное уравнение (1) не может иметь более одного решения.
Задача 2. При каких значениях 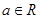 имеет решения уравнение
имеет решения уравнение
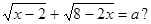 (2)
(2)
Решение: область определения уравнения - отрезок 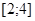 , рассмотрим функцию
, рассмотрим функцию 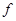 , положив
, положив 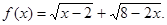
Тогда на открытом промежутке 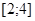
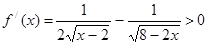
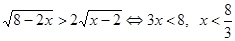 , так что
, так что 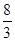 - единственная критическая точка функции
- единственная критическая точка функции 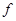 , являющаяся, очевидно, точкой максимума. Поскольку
, являющаяся, очевидно, точкой максимума. Поскольку 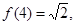
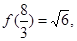 то
то 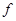 примет наибольшее значение при
примет наибольшее значение при 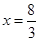 , а наименьшее значение - при
, а наименьшее значение - при 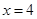 .
.
Так как функция 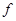 непрерывна, то её область значений представляет собой отрезок
непрерывна, то её область значений представляет собой отрезок 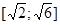 , между её наименьшим и наибольшим значением. Другими словами, исходное уравнение (2) имеет решения при
, между её наименьшим и наибольшим значением. Другими словами, исходное уравнение (2) имеет решения при 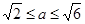 .
.
|
|
|
 2015-07-14
2015-07-14 2071
2071
