Лекция 10
Если в линейном однородном уравнении
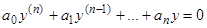 (1)
(1)
все коэффициенты 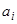 постоянны, то его частные решения могут быть найдены в виде
постоянны, то его частные решения могут быть найдены в виде 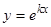 , где
, где  — постоянная. Действительно, подставляя в уравнение (1)
— постоянная. Действительно, подставляя в уравнение (1) 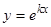 и
и 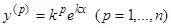 , будем иметь
, будем иметь 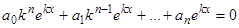 . Сокращая на необращающийся в нуль множитель
. Сокращая на необращающийся в нуль множитель 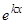 , получим так называемое характеристическое уравнение
, получим так называемое характеристическое уравнение
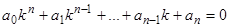 . (2)
. (2)
Это уравнение 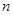 -й степени определяет те значения
-й степени определяет те значения  , при которых
, при которых 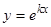 является решением исходного линейного однородного уравнения с постоянными коэффициентами (1). Если все корни
является решением исходного линейного однородного уравнения с постоянными коэффициентами (1). Если все корни 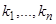 характеристического уравнения различны, то, тем самым, найдено
характеристического уравнения различны, то, тем самым, найдено 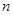 линейно независимых решений
линейно независимых решений 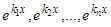 уравнения (1). Следовательно,
уравнения (1). Следовательно, 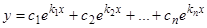 , где
, где 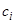 — произвольные постоянные, является общим решением исходного уравнения (1).
— произвольные постоянные, является общим решением исходного уравнения (1).
Пример 1. 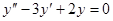 . Характеристическое уравнение имеет вид
. Характеристическое уравнение имеет вид 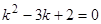 , его корни
, его корни 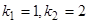 . Следовательно, общее решение исходного уравнения имеет вид
. Следовательно, общее решение исходного уравнения имеет вид 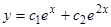 .
.
Пример 2. 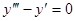 . Характеристическое уравнение
. Характеристическое уравнение 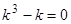 имеет корни
имеет корни 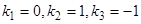 . Общее решение рассматриваемого уравнения
. Общее решение рассматриваемого уравнения 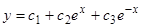 .
.
Теорема. Если линейное однородное уравнение 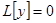 с действительными коэффициентами
с действительными коэффициентами 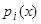 имеет комплексное решение
имеет комплексное решение  , то действительная часть этого решения
, то действительная часть этого решения 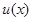 и его мнимая часть
и его мнимая часть 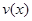 в отдельности являются решениями того же однородного уравнения.
в отдельности являются решениями того же однородного уравнения.
Доказательство. Дано 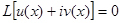 . Надо доказать, что
. Надо доказать, что 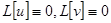 .
.
Пользуясь двумя свойствами линейного оператора, получим 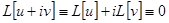 , откуда
, откуда 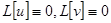 , так как комплексная функция действительной переменной обращается тождественно в нуль тогда и только тогда, когда ее действительная и мнимая части тождественно равны нулю.
, так как комплексная функция действительной переменной обращается тождественно в нуль тогда и только тогда, когда ее действительная и мнимая части тождественно равны нулю.
Мы применили два свойства оператора 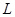 к комплексной функции
к комплексной функции 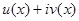 действительной переменной, что, очевидно, допустимо, так как при доказательстве двух свойств были использованы лишь следующие свойства производных:
действительной переменной, что, очевидно, допустимо, так как при доказательстве двух свойств были использованы лишь следующие свойства производных: 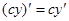 , где
, где  — постоянная, и
— постоянная, и 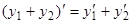 , остающиеся справедливыми и для комплексных функций действительной переменной.
, остающиеся справедливыми и для комплексных функций действительной переменной.
Так как коэффициенты уравнения (1) предполагаются действительными, то комплексные корни характеристического уравнения могут появляться лишь сопряженными парами. Комплексные решения 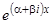 и
и 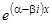 , соответствующие паре комплексных сопряженных корней
, соответствующие паре комплексных сопряженных корней 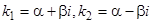 , могут быть заменены двумя действительными решениями: действительной и мнимой частями одного из решений:
, могут быть заменены двумя действительными решениями: действительной и мнимой частями одного из решений: 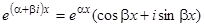 или
или 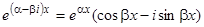 . Таким образом, паре комплексных сопряженных корней
. Таким образом, паре комплексных сопряженных корней 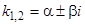 соответствуют два действительных решения:
соответствуют два действительных решения: 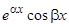 и
и 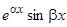 .
.
Пример 3. 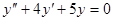 . Характеристическое уравнение имеет вид
. Характеристическое уравнение имеет вид 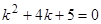 , его корни
, его корни 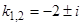 . Общее решение
. Общее решение 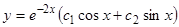 .
.
Пример 4. 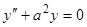 . Характеристическое уравнение
. Характеристическое уравнение 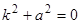 имеет корни
имеет корни 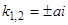 . Общее решение
. Общее решение 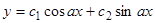 .
.
Если среди корней характеристического уравнения имеются кратные, то число различных решений вида 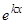 меньше
меньше 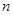 и, следовательно, недостающие линейно независимые решения надо искать в ином виде.
и, следовательно, недостающие линейно независимые решения надо искать в ином виде.
Докажем, что если характеристическое уравнение имеет корень 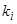 кратности
кратности 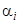 , то решениями исходного уравнения будет не только
, то решениями исходного уравнения будет не только 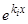 , но и
, но и 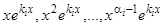 .
.
Предположим вначале, что характеристическое уравнение имеет корень 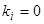 кратности
кратности 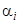 . Следовательно, левая часть характеристического уравнения (2) имеет в этом случае общий множитель
. Следовательно, левая часть характеристического уравнения (2) имеет в этом случае общий множитель 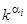 , т.е. коэффициенты
, т.е. коэффициенты 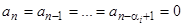 , и характеристическое уравнение имеет вид
, и характеристическое уравнение имеет вид 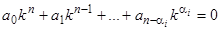 . Соответствующее линейное однородное дифференциальное уравнение
. Соответствующее линейное однородное дифференциальное уравнение 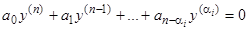 , очевидно, имеет частные решения
, очевидно, имеет частные решения 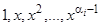 , так как уравнение не содержит производных порядка ниже чем
, так как уравнение не содержит производных порядка ниже чем 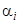 . Итак, кратному корню
. Итак, кратному корню 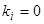 кратности
кратности 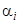 соответствует
соответствует 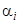 линейно независимых решений
линейно независимых решений 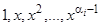 .
.
Если характеристическое уравнение имеет корень 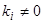 кратности
кратности 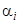 , то замена переменных
, то замена переменных
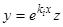 (3)
(3)
сводит задачу к уже рассмотренному случаю равного нулю кратного корня.
Действительно, линейное однородное преобразование неизвестной функции (3) сохраняет линейность и однородность уравнения. Постоянство коэффициентов при замене переменных (3) также сохраняется, так как 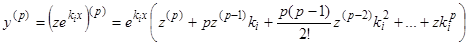 , и после подстановки в уравнение (1) и сокращения на
, и после подстановки в уравнение (1) и сокращения на 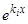 при
при 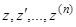 остаются лишь постоянные коэффициенты.
остаются лишь постоянные коэффициенты.
Итак, преобразованное уравнение будет линейным однородным уравнением 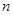 -го порядка с постоянными коэффициентами
-го порядка с постоянными коэффициентами
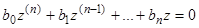 , (4)
, (4)
причем корни характеристического уравнения
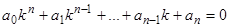 . (2)
. (2)
отличаются от корней характеристического уравнения для преобразованного уравнения (4)
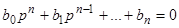 (5)
(5)
на слагаемое 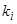 , так как между решениями
, так как между решениями 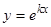 уравнения (1) и
уравнения (1) и 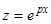 уравнения (4) должна быть зависимость
уравнения (4) должна быть зависимость 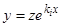 или
или  , откуда
, откуда 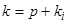 . Следовательно, корню
. Следовательно, корню 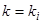 уравнения (2) соответствует корень
уравнения (2) соответствует корень 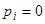 уравнения (5).
уравнения (5).
Как нетрудно проверить, при этом соответствии сохранится и кратность корня, т.е. корень 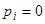 будет иметь кратность
будет иметь кратность 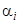 .
.
Действительно, кратный корень 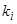 уравнения (2) можно рассматривать как результат совпадения различных корней этого уравнения при изменении его коэффициентов, но тогда в силу зависимости
уравнения (2) можно рассматривать как результат совпадения различных корней этого уравнения при изменении его коэффициентов, но тогда в силу зависимости 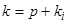 совпадут с
совпадут с 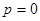 и
и 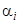 корней уравнения (5).
корней уравнения (5).
Корню 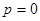 кратности
кратности 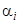 соответствуют частные решения
соответствуют частные решения 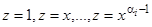 . Следовательно, в силу зависимости
. Следовательно, в силу зависимости 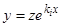 , корню
, корню 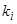 кратности
кратности 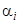 уравнения (2) будут соответствовать
уравнения (2) будут соответствовать 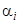 частных решений
частных решений
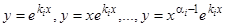 . (6)
. (6)
Можно показать, что решения
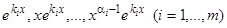 , (7)
, (7)
где 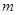 — число различных корней
— число различных корней 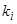 характеристического уравнения, линейно независимы.
характеристического уравнения, линейно независимы.
Следовательно, общее решение уравнения (1) имеет вид  , где
, где 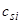 — произвольные постоянные.
— произвольные постоянные.
Пример 5. 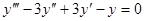 . Характеристическое уравнение
. Характеристическое уравнение 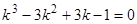 или
или 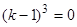 имеет трехкратный корень
имеет трехкратный корень 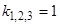 . Следовательно, общее решение имеет вид
. Следовательно, общее решение имеет вид 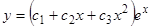 .
.
Если характеристическое уравнение имеет кратный комплексный корень 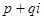 кратности
кратности  , то соответствующие ему решения
, то соответствующие ему решения 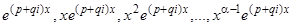 можно преобразовать по формулам Эйлера
можно преобразовать по формулам Эйлера 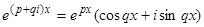 и, отделяя действительную и мнимую части, получить
и, отделяя действительную и мнимую части, получить 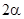 действительных решений:
действительных решений:
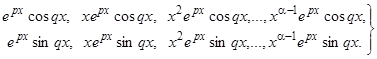 (8)
(8)
Взяв действительные и мнимые части решений, соответствующих сопряженному корню 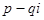 характеристического уравнения, мы не получим новых линейно независимых решений. Таким образом, паре комплексных сопряженных корней
характеристического уравнения, мы не получим новых линейно независимых решений. Таким образом, паре комплексных сопряженных корней 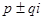 кратности
кратности  соответствуют
соответствуют 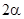 линейно независимых действительных решений (8).
линейно независимых действительных решений (8).
Пример 6. 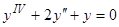 . Характеристическое уравнение
. Характеристическое уравнение 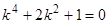 или
или 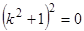 имеет двукратные корни
имеет двукратные корни 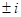 . Следовательно, общее решение имеет вид
. Следовательно, общее решение имеет вид 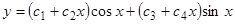 .
.
 2014-02-02
2014-02-02 5302
5302
