Экспериментально были получены изотермы адсорбции различных ПАВ. Все они имели одинаковую форму – имелся горизонтальный участок (рис. 11). Для веществ одного гомологического ряда все изотермы в пределе сливаются (рис. 12.). Это может быть при условии, что: 1) все молекулы гомологического ряда, независимо от длины углеводородной цепи, занимают на поверхности раздела фаз одинаковую площадь; 2) адсорбционный слой имеет толщину не более одной молекулы, т.е. мономолекулярный.
 | |||
 | |||
,
|
Уравнение Гиббса не описывает всю экспериментально полученную изотерму адсорбции. Напомним, что оно работает только при малых концентрациях ПАВ. Изотермы мономолекулярной адсорбции хорошо описывает уравнение Ленгмюра.
Уравнение Ленгмюра было выведено для адсорбции газа на твердой поверхности, но оно применимо и для описания адсорбции на границе раздела раствор ПАВ-воздух. Более того, именно для границы твердое тело-газ, для которой оно было выведено, чаще наблюдаются различного рода отклонения от ленгмюровской изотермы адсорбции.
Основные положения теории Ленгмюра будут приведены при рассмотрении адсорбции на твердой поверхности. В настоящей главе ограничимся только выводом уравнения.
Рассмотрим поверхность раздела жидкость-газ площадью 1 м2.
Пусть Q – площадь поверхности, занятая молекулами ПАВ;
(1- Q) – свободная площадь;
n а – число адсорбирующихся в единицу времени частиц (молекул);
n д – число десорбирующихся частиц.
При равновесии скорость адсорбции равна скорости десорбции, т.е.
n а = n д.
Скорость адсорбции пропорциональна доле свободной площади поверхностного слоя и концентрации ПАВ в растворе
n а = k а с (1- Q),
скорость десорбции зависит только от доли площади поверхности, заполненной молекулами ПАВ:
n д = k д Q.
Тогда
k а с (1- Q) = k д Q.
Решаем относительно Q:
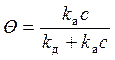 .
.
Разделим числитель и знаменатель на k д:
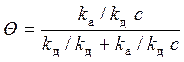 ,
,
k а/ k д = k – константа адсорбционно-десорбционного равновесия,
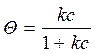 . (10)
. (10)
Установим связь между Q, Г и Г max.
Площадь поверхностного слоя, заполненную молекулами ПАВ, можно найти как произведение площади, занимаемой одной молекулой ПАВ S 0, на количество молекул в поверхностном слое N = nNa, где n – количество вещества в поверхностном слое, Na – число Авогадро, Na = 6,02×1023 моль-1.
Количество вещества, отнесенное к единице площади поверхностного слоя, есть адсорбция Г данного вещества. Поскольку при выводе уравнения рассматривается поверхностный слой площадью 1 м2, n = Г. При насыщении поверхностного слоя молекулами ПАВ Q = 1 м2 n = Г max.
Тогда
S 0 Г Na = Q,
S 0 Г max Na = 1,
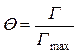 .
.
Подставим в уравнение (10):
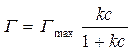 . (11)
. (11)
Уравнение (11) – уравнение Ленгмюра, описывающее изотерму мономолекулярной адсорбции.
При очень маленьких концентрациях ПАВ kc << 1, уравнение Ленгмюра принимает вид уравнения прямой и описывает прямолинейный участок изотермы адсорбции (до перегиба):
Г = Г max kc.
При больших концентрациях kc >> 1 и Г = Г max – горизонтальный участок изотермы адсорбции.
Таким образом, в отличие от уравнения Гиббса, уравнение Ленгмюра описывает всю изотерму адсорбции.
Для нахождения констант уравнения Ленгмюра Г max и k его приводят к линейному виду. После линеаризации
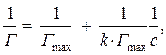
где у = 1/Г, х = 1/С, 1/ Г max = a (свободный член), 1/ k Г max = b (угловой коэффициент)
 Строят график в координатах
Строят график в координатах
1/ Г = f(1/ с) (рис. 13). По графику определяют свободный член а и угловой коэффициент b (тангенс угла наклона tg a), по которым находят значения Г max и k.
Зная предельную адсорбцию Г max, можно рассчитать длину молекулы ПАВ l и площадь, занимаемую одной молекулой в поверхностном слое S 0.
На поверхности раздела фаз площадью 1 м2 находится Г max Nа молекул поверхностно-активного вещества.
В состоянии плотнейшей упаковки, соответствующем насыщенному поверхностному слою, эти частицы занимают площадь Г max NаS 0 = 1.
Поэтому
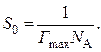
Объем насыщенного поверхностного слоя, соответствующий площади 1 м2, равен, с одной стороны, Г max× М /r и 1× l – с другой. Последнее утверждение правильно, если принять, что толщина поверхностной зоны равна длине молекулы l. В этом случае выполняется равенство
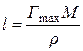 ,
,
где М – молярная масса ПАВ; r – плотность поверхностно-активного вещества.
При малых концентрациях ПАВ расчет адсорбции по уравнениям Гиббса и Ленгмюра дает близкие результаты, т.е. правые части этих уравнений можно приравнять:
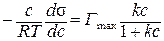 ,
,
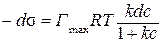 .
.
Интегрируя в определенных пределах от 0 до с и от s 0 до s, получим:
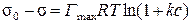 .
.
Сопоставляя полученное уравнение с уравнением Шишковского (1), легко установить связь между константами двух уравнений:
B = Г max RT,
а константа k в уравнениях Шишковского и Ленгмюра – это константа адсорбционно-десорбционного равновесия.
 2014-02-02
2014-02-02 5675
5675
