Найдем абсциссу точки пересечения кривых:
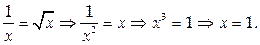
Вычислим их производные при х = 1:
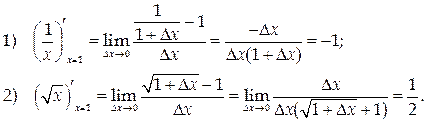
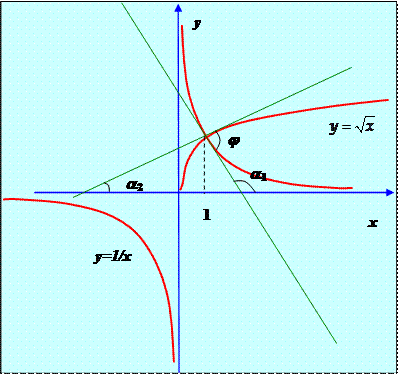
Если a 1 и a 2 – углы, образованные касательными к графикам данных функций при х = 1 с осью Ох, то тангенс угла j между касательными (и соответственно между кривыми) можно найти по формуле тангенса разности:
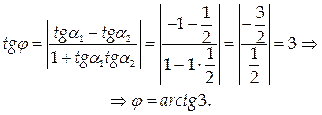
Ответ: arctg 3.
1.2.2. Свойства производной. Таблица производных
Правила дифференцирования
Пусть при рассматриваемых значениях х существуют производные функций f(x) и g(x), то есть эти функции являются дифференцируемыми при данных значениях аргумента. Сформулируем и докажем некоторые свойства производных.
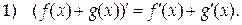
Доказательство.
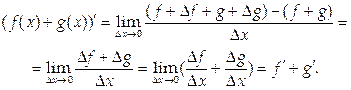
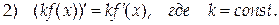
Доказательство.
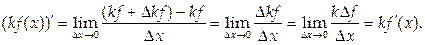
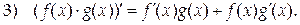
Доказательство.
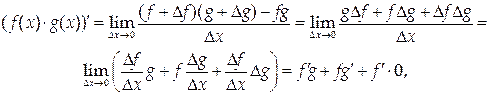
так как 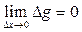 в силу непрерывности g(x).
в силу непрерывности g(x).
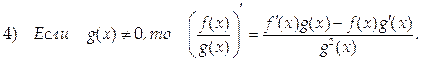
Доказательство.
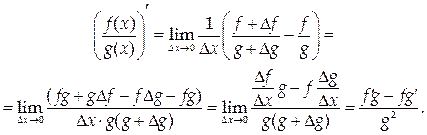
Производная сложной функции
Если функция u = j(x) имеет при некотором значении х производную ux’=j’(x), а функция y = f(u) имеет при соответствующем значении u производную yu’= f’(u), то сложная функция y = f(j(x)) тоже имеет при данном значении х производную, равную
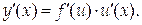
Доказательство.
Так как
|
|
|
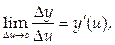
то по третьему определению предела можно представить
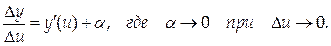
Тогда
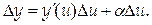
Разделив обе части равенства на Dх, получим:
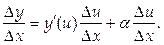
Переходя к пределу при 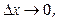 получаем:
получаем:
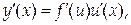
так как 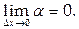
Производная обратной функции
Если для функции y=f(x) существует обратная функция х=j(у), которая в некоторой точке у имеет производную j’(у)≠0, то в соответствующей точке х функция f(x) тоже имеет производную, причем
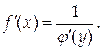
Доказательство.
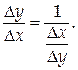
Так как j(у) непрерывна,
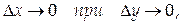
и при переходе к пределу при 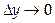 получаем:
получаем:
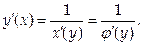
Инвариантность формы дифференциала
Найдем выражение для дифференциала сложной функции. Пусть y=f(u), u=j(x), то есть y=f(j(x)). Тогда
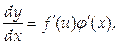
следовательно,
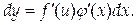
Но
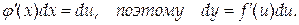
Таким образом, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство называется свойством неизменности, или инвариантности, дифференциала.
Производные основных элементарных функций
Используя полученные формулы и свойства производных, найдем производные основных элементарных функций.
1. Если f(x)=C=const, то ΔС=0, поэтому С΄=0.
2. у=xn, где n – натуральное число. Тогда по формуле бинома Ньютона можно представить
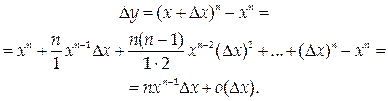
Следовательно, у΄ = nxn-1.
3. y = sin x,
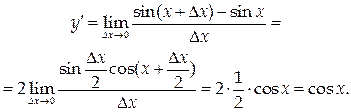
4. y = cos x,
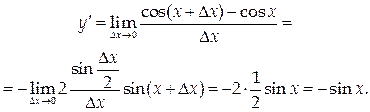
5. y = tg x,
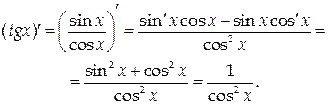
6. Аналогично можно получить формулу
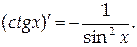
7. 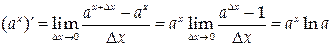
(см. 2-е следствие из второго замечательного предела).
8. 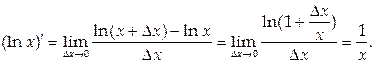
(см. 1-е следствие из второго замечательного предела).
9. 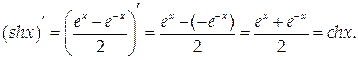
Таким же образом можно найти производные остальных гиперболических функций.
10. По формуле производной обратной функции
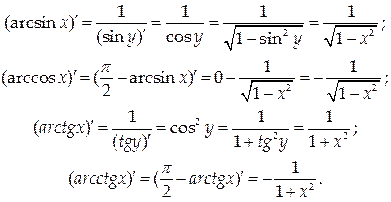 .
.
11. Если a – произвольное действительное число, то
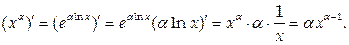
В результате получена таблица основных производных:
| № | f(x) | f΄(x) | № | f(x) | f΄(x) |
| C | ctgx | 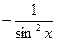
| |||
| xα | αxα-1 | shx | chx | ||
| ax | axlna | chx | shx | ||
| ex | ex | thx | 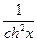
| ||
| lnx | 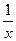
| cthx | 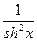
| ||
| sinx | cosx | arcsinx | 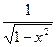
| ||
| cosx | -sinx | arccosx | 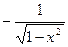
| ||
| tgx | 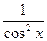
| arctgx | 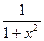
| ||
| arcctgx | 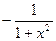
|
Логарифмическое дифференцирование
|
|
|
Иногда полезно использовать так называемую формулу логарифмического дифференцирования. Пусть f(x)>0 на некотором множестве значений аргумента и дифференцируема на этом множестве. Тогда по формуле производной сложной функции
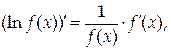
откуда
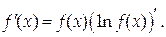
|
Эту формулу удобно использовать в тех случаях, когда производную натурального логарифма данной функции найти проще, чем производную самой функции.
Примеры.
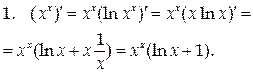
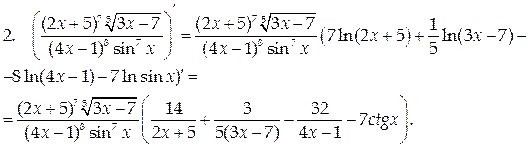
Дифференцирование функций, заданных параметрически
Если функция y = f(x) задана в виде:
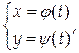
причем функция j(t) имеет обратную функцию t = Φ(x), то у = y(Φ(х)), и
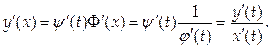
Полученная формула дает возможность находить производную функции, заданной параметрически, без определения непосредственной зависимости у от х.
Пример.
х = а(1 – cos t), y = a(t – sin t) – параметрические уравнения кривой, называемой циклоидой. Найдем у΄(х):
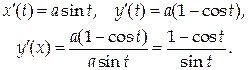
 2015-07-14
2015-07-14 510
510








