Примеры

1. Покажем, что функция

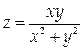
не имеет предела при М, стремящемся к О (0,0). Действительно, если в качестве линии, по которой точка М приближается к началу координат, выбрать прямую у = х, то на этой прямой

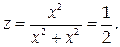
Если же траекторией движения считать прямую у = 2 х, то

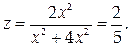
Следовательно, предел в точке (0,0) не существует.

2. Найдем повторные пределы функции

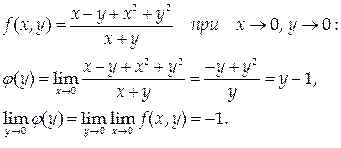
Если же произвести предельные переходы в обратном порядке, получим:

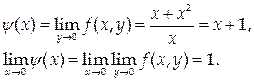
Таким образом, повторные пределы оказались различными (откуда следует, конечно, что функция не имеет в точке (0,0) предела в обычном смысле).

Замечание. Можно доказать, что из существования предела в данной точке в обычном смысле и существования в этой точке пределов по отдельным аргументам следует существование и равенство повторных пределов. Обратное утверждение неверно.

Функция 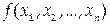называется непрерывной в точке М 0 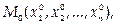если

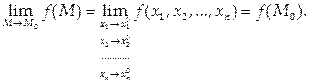
Если ввести обозначения

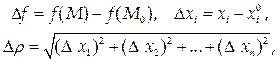
то это условие можно переписать в форме

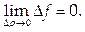
Внутренняя точка М0 области определения функции z = f (M) называется точкой разрыва функции, если в этой точке не выполняется условие

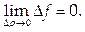
Замечание. Множество точек разрыва может образовывать на плоскости или в пространстве линии или поверхности разрыва.

Примеры.

1. Функция z = x ² + y ² непрерывна в любой точке плоскости О ху. Действительно,

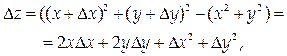
поэтому

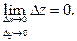
2. Единственной точкой разрыва функции

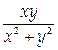
является точка (0,0).

3. Для функции

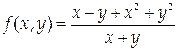
линией разрыва является прямая х + у = 0.

Свойства пределов и непрерывных функций

Так как определения предела и непрерывности для функции нескольких переменных практически совпадает с соответствующими определениями для функции одной переменной, то для функций нескольких переменных сохраняются все свойства пределов и непрерывных функций, доказанные в первой части курса, а именно:

1) Если существуют

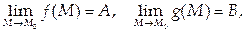
то существуют и

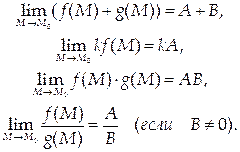
2) Если

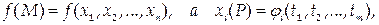
и для любого i существуют пределы

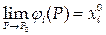
и существует

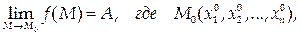
то существует и предел сложной функции

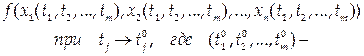
координаты точки Р ₀.

3) Если функции f(M) и g(M) непрерывны в точке М ₀, то в этой точке непрерывны и функции f(M) + g(M), kf(M), f(M)·g(M), f(M)/g(M) (если g(M ₀) не равно нулю).

4) Если функции

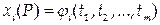
непрерывны в точке

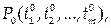
а функция

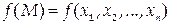
непрерывна в точке

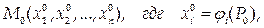
то сложная функция

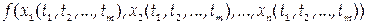
непрерывна в точке Р₀.

5) Функция

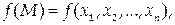
непрерывная в замкнутой ограниченной области D, принимает в этой области свое наибольшее и наименьшее значения.

6) Если функция

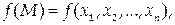
непрерывная в замкнутой ограниченной области D, принимает в этой области значения А и В, то она принимает в области D и любое промежуточное значение, лежащее между А и В.

7) Если функция

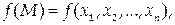
непрерывная в замкнутой ограниченной области D, принимает в этой области значения разных знаков, то найдется по крайней мере одна точка из области D, в которой f = 0.