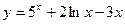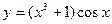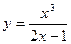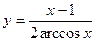Нахождение производных функций
Производной функции 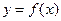 в точке
в точке 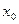 называется предел отношения приращения
называется предел отношения приращения 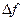 функции в этой точке к приращению
функции в этой точке к приращению 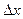 аргумента, когда приращение аргумента стремится к нулю:
аргумента, когда приращение аргумента стремится к нулю:
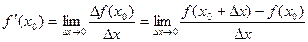 .
.
Функция 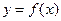 , имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
Производная функции 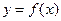 обозначается
обозначается 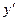 ,
, 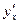 ,
, 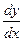 или
или 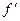 ,
, 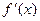 ,
, 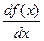 .
.
Нахождение производной называется дифференцированием.
Правила дифференцирования
1. 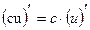 , c – const,
, c – const,
2. 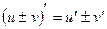
3. 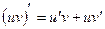 , где
, где 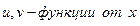
4. 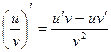
Таблица производных элементарных функций
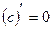 , c - const , c - const
| 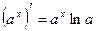
|
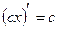
| 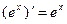
|
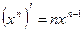
| 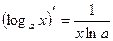
|
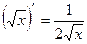
| 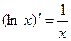
|
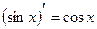
| 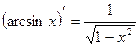
|
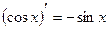
| 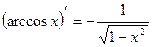
|
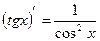
| 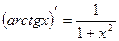
|
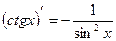
| 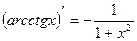
|
| Вариант 0 |
| Найдите производные функций: |
Решение:
1) Запишем данную функцию 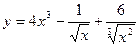 следующим образом:
следующим образом:
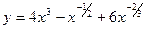 .
.
Тогда 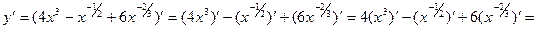
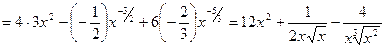 .
.
2) 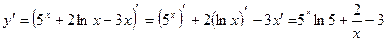 (применили правила дифференцирования 2 и 1).
(применили правила дифференцирования 2 и 1).
3) 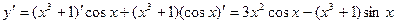 (применили правило дифференцирования 3).
(применили правило дифференцирования 3).
.
4) 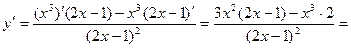
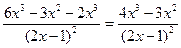 (применили правила дифференцирования 4 и 1).
(применили правила дифференцирования 4 и 1).
5) 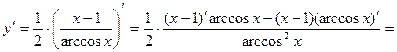
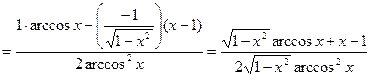 (применили правила дифференцирования 4 и 1).
(применили правила дифференцирования 4 и 1).
 2015-07-14
2015-07-14 331
331