Задача о вычислении скорости движущейся точки

Задачи, приводящие к понятию производной

Рассмотрим прямолинейное неравномерное движение некоторой материальной точки M. Расстояние S, на которое переместится точка M от начального положения 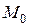за промежуток времени t, будет являться функцией времени 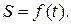Пусть в некоторый момент t точка M находилась на расстоянии S, а в некоторый следующий момент 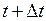точка M находилась на расстоянии 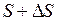от начального положения 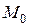. Таким образом, за величину времени 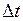величина S получила приращение 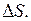Отношение 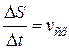дает среднюю скорость движения точки M за время Δ t. Средняя скорость зависит от промежутка времени Δ t и не может дать нам правильное представление об истинной скорости движения точки в момент t. Для более точного представления об истинной скорости движения в момент времени t необходимо взять как можно меньший промежуток времени Δ t. Наиболее полно характеризует скорость движения точки в момент времени t тот предел, к которому стремится средняя скорость при 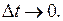Этот предел называют скоростью движения в данный момент:

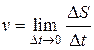(1)

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Δ S к приращению времени Δ t, когда приращение времени Δ t стремится к нулю.

Учитывая, что 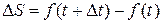равенство (1) запишем в виде:

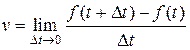(2)

Это и будет скорость неравномерного движения.