Задача о проведении касательной к кривой

Пусть дана кривая К и на ней точка М (рис. 1). Возьмем на кривой ещё какую-нибудь точку 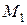и проведем секущую 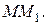Когда точка 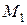будет перемещаться вдоль кривой, эта секущая будет вращаться вокруг точки M.

О п р е д е л е н и е. Касательной к кривой К в точке М называется предельное положение МТ секущей 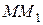, когда точка 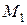вдоль по кривой стремится к совпадению с M.

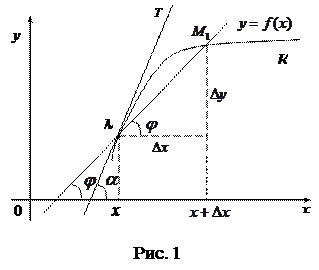Для определения положения касательной к кривой в точке М достаточно знать угловой коэффициент касательной в точке M. Для любой кривой с уравнением 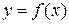угловой коэффициент устанавливается следующим образом. Приращению абсциссы Δ x отвечает приращение Δ y ординаты. Отношение выражает угловой коэффициент секущей tgφ. Угловой коэффициент k = tgα касательной в точке M получается путем перехода к пределу при Δ x → 0:

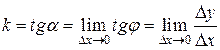(3)

Таким образом, угловой коэффициент касательной к кривой выражается как предел отношения приращения ординаты точки Δ y к приращению абсциссы точки Δ x, когда приращение абсциссы Δ x стремится к нулю.