1. Пусть у = у (х) – некоторая функция, c = const. Постоянный множитель может быть вынесен за знак производной: 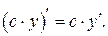
2. Пусть функции u и v имеют производные в некоторой точке. Тогда в этой же точке производная суммы либо разности функций равна сумме либо разности производных: 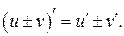
3. Пусть функции u и v имеют производные в некоторой точке.
Тогда в этой же точке производная произведения двух дифференцируемых функций существует и равна произведению производной первой функции на вторую плюс произведение первой функции на производную второй функции: 
4. Пусть функции u и v имеют производные в некоторой точке и кроме того v не равно нулю. Тогда в этой же точке производная дроби (т.е. частного от деления двух функций) существует и равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя: 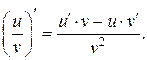
П р и м е р 2. Найти производные функций:
а) 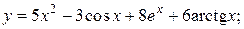 б)
б)  в)
в) 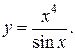
Решение.
а) Учитывая, что постоянный множитель может быть вынесен за знак производной и что производная суммы либо разности функций равна сумме либо разности производных (правила дифференцирования 1 и 2), получим: 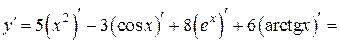 (воспользуемся таблицей производных) =
(воспользуемся таблицей производных) = 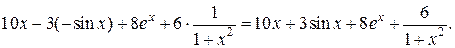
б) Учитывая правило 3, получим:

в) Учитывая правило 4, получим:
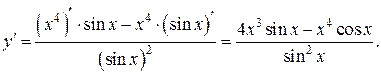
 2015-07-14
2015-07-14 823
823








