Пусть 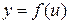 и
и 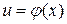 , тогда
, тогда 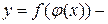 сложная функция с промежуточным аргументом
сложная функция с промежуточным аргументом 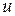 и независимым аргументом х.
и независимым аргументом х.
Если функция 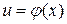 имеет производную
имеет производную 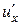 в точке х, а функция
в точке х, а функция 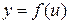 имеет производную
имеет производную 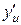 в соответствующей точке
в соответствующей точке 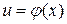 , то сложная функция
, то сложная функция 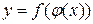 имеет производную
имеет производную 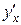 в точке х, которая находится по формуле:
в точке х, которая находится по формуле:
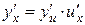 (6)
(6)
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по независимому аргументу.
П р и м ер 3. Найти производные сложных функций:
а) 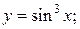 б)
б) 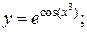 в)
в) 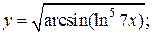 г)
г) 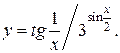
Решение.
а) Функция 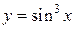 является сложной, здесь
является сложной, здесь 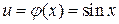 и
и 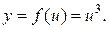 Другими словами, функция такова, что она является степенью
Другими словами, функция такова, что она является степенью 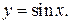 Найдем производную степени (таблица производных): это показатель степени, умноженный на то, что в степень возводится, в степени на единицу меньше. Поскольку в степень возводится функция, зависящая от x, необходимо предыдущий результат умножить на производную sin x (формула 6). Таким образом, получим:
Найдем производную степени (таблица производных): это показатель степени, умноженный на то, что в степень возводится, в степени на единицу меньше. Поскольку в степень возводится функция, зависящая от x, необходимо предыдущий результат умножить на производную sin x (формула 6). Таким образом, получим: 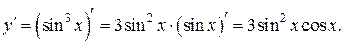
Итак, 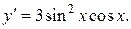
б) Данная функция является сложной. Показатель степени у показательной функции это 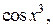 а аргументом тригонометрической функции является
а аргументом тригонометрической функции является 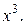 Применяя последовательно правило дифференцирования сложной функции (формула 6), получим:
Применяя последовательно правило дифференцирования сложной функции (формула 6), получим: 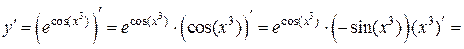
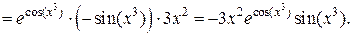 Итак,
Итак, 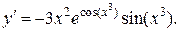
в) Применяя последовательно правило дифференцирования сложной функции (формула 6), получим: 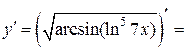

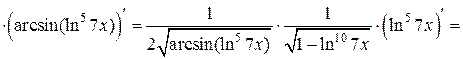

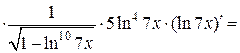
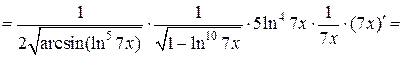
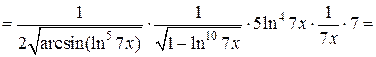
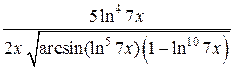 .
.
Итак, 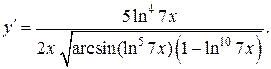
г) Найдем производную данной функции по правилу дифференцирования частного двух функций (правило 4): 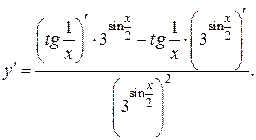
Функции 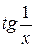 и
и 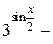 сложные, найдем их производные по правилу дифференцирования сложной функции (формула 6):
сложные, найдем их производные по правилу дифференцирования сложной функции (формула 6):
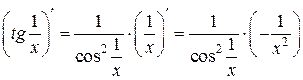 ,
, 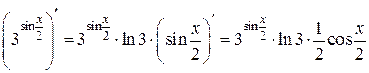 .
.
Подставим вычисленные производные в формулу для производной частного и запишем производную от заданной функции в виде:
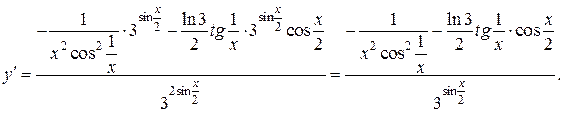
 2015-07-14
2015-07-14 865
865








