Выражение  , являющееся производной по x от натурального логарифма данной функции
, являющееся производной по x от натурального логарифма данной функции  , называется логарифмической производной. Применение логарифмической производной значительно упрощает дифференцирование в случаях, когда
, называется логарифмической производной. Применение логарифмической производной значительно упрощает дифференцирование в случаях, когда
1) сложная функция  является показательно-степенной, т.е. у которой и основание и показатель степени являются функциями от x:
является показательно-степенной, т.е. у которой и основание и показатель степени являются функциями от x:  .
.
2) функция  представлена в виде произведения большого количества сомножителей.
представлена в виде произведения большого количества сомножителей.
Применение логарифмической производной состоит из следующих приёмов:
1. Необходимо прологарифмировать функцию  :
: 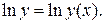
2. Преобразовать правую часть записанного равенства, пользуясь свойствами логарифмов: 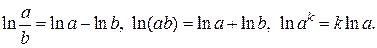
3. Продифференцировать полученное равенство, учитывая, что 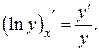
4. Выразить из этого равенства искомое выражение y ´, учитывая, что 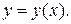
П р и м е р 4. Найти производные показательно-степенных функций:
а)  б)
б) 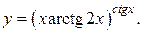
Решение.
а) Логарифмируя функцию и используя свойства логарифмов, получаем:  Дифференцируя полученное равенство по x, будем иметь:
Дифференцируя полученное равенство по x, будем иметь:  Умножая на y и подставляя
Умножая на y и подставляя  вместо y, получаем:
вместо y, получаем:  .
.
б) Логарифмируя функцию и используя свойства логарифмов, получаем:  или
или  . Дифференцируем полученное равенство по переменной x:
. Дифференцируем полученное равенство по переменной x:
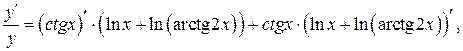
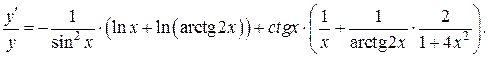
Умножая на y и подставляя  вместо y, получаем:
вместо y, получаем:
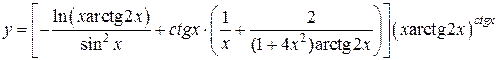
П р и м е р 5. Найти производную функции  используя логарифмическую производную.
используя логарифмическую производную.
Решение.
Логарифмируя функцию и используя свойства логарифмов, получим:  Дифференцируя полученное равенство по x, будем иметь:
Дифференцируя полученное равенство по x, будем иметь: 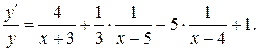
Умножая на y и подставляя  вместо y, получим:
вместо y, получим:
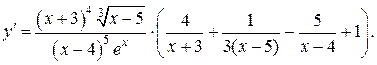
 2015-07-14
2015-07-14 636
636








