Пусть значения двух переменных связаны между собой некоторым уравнением, которое символически может быть обозначено в виде:
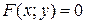 . (7)
. (7)
Если функция 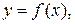 определённая в некотором промежутке, при подстановке в это уравнение, обращает его в тождество, то уравнение задаёт неявную функцию. Термины «явная функция» и «неявная функция» характеризуют способ задания функции. Каждая явная функция
определённая в некотором промежутке, при подстановке в это уравнение, обращает его в тождество, то уравнение задаёт неявную функцию. Термины «явная функция» и «неявная функция» характеризуют способ задания функции. Каждая явная функция 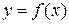 может быть представлена как неявная в виде
может быть представлена как неявная в виде 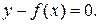
Производную 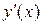 неявно заданной функции можно найти, продифференцировав уравнение (7) (при этом у считается функцией от х) и разрешая затем полученное уравнение относительно
неявно заданной функции можно найти, продифференцировав уравнение (7) (при этом у считается функцией от х) и разрешая затем полученное уравнение относительно 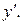
П р и м е р 6. Найти производные функций, заданных неявно уравнениями:
а) 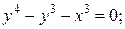 б)
б) 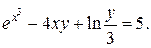
Решение.
а) Если y является функцией от x, то это равенство является тождеством. Дифференцируя обе части этого тождества по х, считая, что y является функцией, зависящей от х, и, пользуясь правилом дифференцирования сложной функции (правило 4), получим: 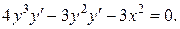
Преобразовывая полученное равенство, выразим производную y ´: 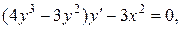
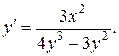
б) Продифференцируем обе части уравнения, рассматривая у как функцию от х, получим: 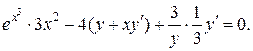 Выразим производную y ´:
Выразим производную y ´: 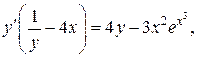
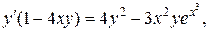
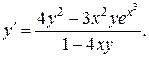
 2015-07-14
2015-07-14 2109
2109
