Пусть функция y от x задана параметрическими уравнениями:
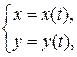 где
где 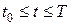 (9)
(9)
Предположим, что функции x (t), y (t) имеют производные. Тогда производную y ´ от функции, заданной параметрически, не находя выражения непосредственной зависимости y от x, можно найти по формуле:
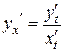 (10)
(10)
П р и м е р 7. Функция y от x задана параметрическими уравнениями: 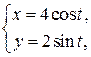 где 0 ≤ t ≤ π. Найти угловой коэффициент касательной к кривой в точке
где 0 ≤ t ≤ π. Найти угловой коэффициент касательной к кривой в точке 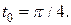
Решение.
Угловой коэффициент касательной к кривой в точке 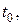 равен значению производной
равен значению производной 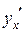 в этой точке. По формуле (10), учитывая, что
в этой точке. По формуле (10), учитывая, что 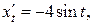
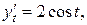 получим:
получим: 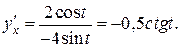 Следовательно, угловой коэффициент касательной к кривой в точке
Следовательно, угловой коэффициент касательной к кривой в точке 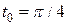 равен
равен 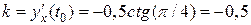 .
.
 2015-07-14
2015-07-14 1024
1024








