Если функция 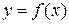 имеет конечную производную на некотором числовом промежутке, так что эта производная представляет новую функцию от x, то может оказаться что эта функция в свою очередь имеет производную. Её называют производной второго порядка или второй производной функции
имеет конечную производную на некотором числовом промежутке, так что эта производная представляет новую функцию от x, то может оказаться что эта функция в свою очередь имеет производную. Её называют производной второго порядка или второй производной функции 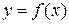 и обозначают одним из символов:
и обозначают одним из символов: 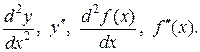
В п. 2 мы говорили, что скорость движения точки v равна производной от пройденного пути 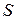 по времени t, а ускорение есть производная от скорости по времени. Значит, ускорение является второй производной от пути
по времени t, а ускорение есть производная от скорости по времени. Значит, ускорение является второй производной от пути 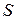 по времени t.
по времени t.
Подобным образом от второй производной можно перейти к третьей, четвертой производной.
О п р е д е л е н и е. Производной n-го порядка или n-ой производной от функции 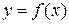 называется производная (первого порядка) от производной (n-1)-го порядка и обозначается в виде:
называется производная (первого порядка) от производной (n-1)-го порядка и обозначается в виде: 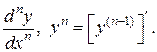
Порядок производной берётся в скобки для того, чтобы его нельзя было принять за показатель степени. Производные четвертого, пятого и высших порядков обозначаются так же с помощью римских цифр без скобок.
П р и м е р 8. Найти производную шестого порядка от функции 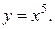
Решение.
Если 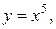 то
то 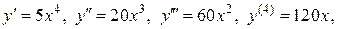
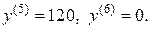
П р и м е р 9. Найти производную второго порядка от функции 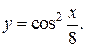
Решение.
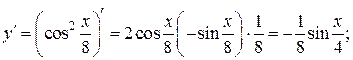
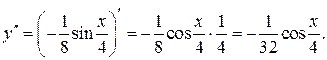
П р и м е р 10. Найти третью производную функции 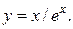
Решение.
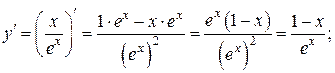
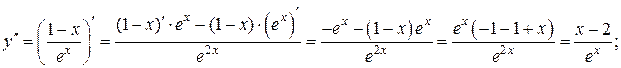
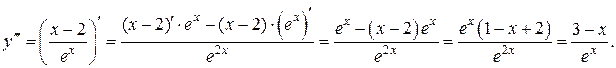
Производная второго порядка от функции, заданной в параметрическом виде находится по формуле:
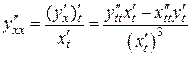 (11)
(11)
П р и м е р 11. Найти вторую производную от функции 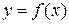 , заданной параметрическими уравнениями
, заданной параметрическими уравнениями 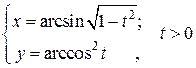
Решение.
Сначала найдем первую производную 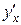 по правилу дифференцирования функции, заданной параметрически (формула 10)
по правилу дифференцирования функции, заданной параметрически (формула 10) 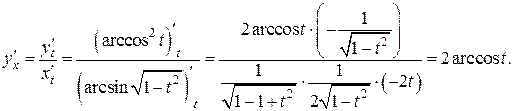 Затем по формуле (11), имеем:
Затем по формуле (11), имеем: 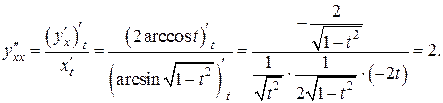
 2015-07-14
2015-07-14 512
512








