Пусть функция 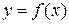 является дифференцируемой на некотором промежутке. По определению производной (формула 7)
является дифференцируемой на некотором промежутке. По определению производной (формула 7) 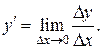 Следовательно, отношение
Следовательно, отношение  при Δ x → 0 отличается от производной
при Δ x → 0 отличается от производной 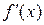 на величину бесконечно малую:
на величину бесконечно малую:  , где
, где  при
при  . Умножая все члены полученного равенства на Δ x, получим
. Умножая все члены полученного равенства на Δ x, получим  .
.
Таким образом, приращение Δ y функции состоит из двух слагаемых, первое из которых есть (при f ´(x) ≠ 0) главная часть приращения, линейная относительно Δ x. Произведение f ´(x)·Δ x называют дифференциалом функции и обозначают через dy или df (x).
О п р е д е л е н и е. Дифференциалом функции 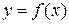 в точке х называется главная часть ее приращения равная произведению производной функции на приращение аргумента:
в точке х называется главная часть ее приращения равная произведению производной функции на приращение аргумента:
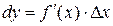
| (12) |
Дифференциал dx независимой переменной x совпадает с приращением Δ x, поэтому формулу (12) можно записать так:
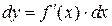
| (13) |
Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
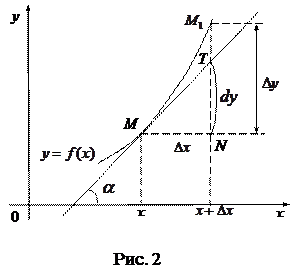 Рассмотрим на графике функции
Рассмотрим на графике функции 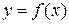 некоторую точку М (x, y) (рис.2), проведем в этой точке касательную к кривой
некоторую точку М (x, y) (рис.2), проведем в этой точке касательную к кривой 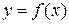 и обозначим через α угол, который образует касательная с положительным направлением оси Ox.
и обозначим через α угол, который образует касательная с положительным направлением оси Ox.
Дадим независимой переменной приращение Δ x, тогда функция получит приращение Δ y. На кривой это точка 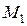 . На чертеже отметим точки Т и N,
. На чертеже отметим точки Т и N, 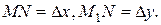 Из прямоугольного треугольника MNT, имеем:
Из прямоугольного треугольника MNT, имеем: 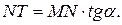 Согласно геометрическому смыслу производной
Согласно геометрическому смыслу производной 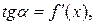 поэтому
поэтому 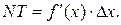 Учитывая, что
Учитывая, что  получим
получим 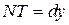 (по формуле 13). Последнее равенство означает, что дифференциал функции y = f (x), соответствующий данным значениям x и Δ x, равен приращению ординаты касательной к кривой
(по формуле 13). Последнее равенство означает, что дифференциал функции y = f (x), соответствующий данным значениям x и Δ x, равен приращению ординаты касательной к кривой 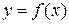 в данной точке x. В этом состоит геометрический смысл дифференциала.
в данной точке x. В этом состоит геометрический смысл дифференциала.
Понятие дифференциала используется в приближенных вычислениях и при решении дифференциальных уравнений.
П р и м е р 12. Вычислить дифференциалы функций:
а)  б)
б) 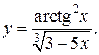
Решение.
а) Используя формулу (13), имеем 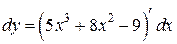

б) Используя формулу (13), имеем 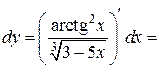
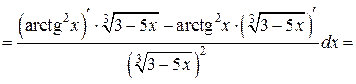
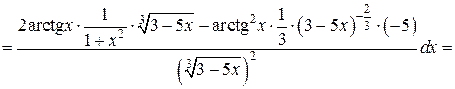

 2015-07-14
2015-07-14 597
597








