Математичний аналіз оперує змінними. Основне поняття – поняття функції. Вектори теж будемо розглядати змінними.
Нагадаємо означення функції, відоме з курсу математичного аналізу.
Якщо кожному елементу x деякої непустої множини X за певним правилом або законом (позначають f, g тощо) ставиться у відповідність єдиний елемент y множини Y, то кажуть, що на множині X визначена функція, яку позначають, наприклад, 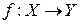 або або 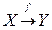 або або 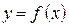 . .
|
Довільний елемент 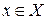 називають незалежною змінною або аргументом, множину X – областю визначення функції
називають незалежною змінною або аргументом, множину X – областю визначення функції 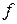 ,множину
,множину 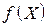 – областю значень функції f:
– областю значень функції f: 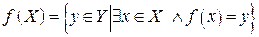
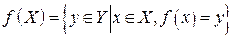 .
.
Область визначення і область значень функції 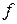 позначають також
позначають також 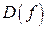 і
і 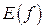 відповідно.
відповідно.
В математичному аналізі, як правило, розглядаються функції, в яких x і y є елементами підмножини множини дійсних чисел  . Такі функції називають числовими або скалярними.
. Такі функції називають числовими або скалярними.
З геометричної точки зору числова функція 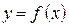 визначає відображення множини точок
визначає відображення множини точок 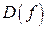 однієї прямої на деяку множину точок
однієї прямої на деяку множину точок 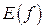 , взагалі кажучи, іншої прямої.
, взагалі кажучи, іншої прямої.
Вектор-функція одного аргументу – функція, в якій залежна змінна 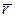 є вектором, а аргумент t приймає значення з множини дійсних чисел
є вектором, а аргумент t приймає значення з множини дійсних чисел 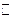 .
.
Функція 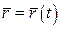 називається вектор-функцією одного скалярного аргументу, якщо кожному значенню називається вектор-функцією одного скалярного аргументу, якщо кожному значенню 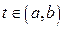 ставиться у відповідність вектор ставиться у відповідність вектор  двовимірного двовимірного 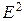 або тривимірного або тривимірного 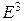 евклідового простору. евклідового простору.
|
Позначення: 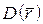 – область визначення
– область визначення  ,
, 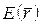 – область значень
– область значень  .
.
У загальному випадку зі зміною t змінюється вектор 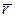 як за величиною, так і за напрямком. Але може бути вектор-функція сталого модуля (змінюється лише напрям, а модуль залишається незмінним) і вектор-функція сталого напряму (змінюється лише модуль).
як за величиною, так і за напрямком. Але може бути вектор-функція сталого модуля (змінюється лише напрям, а модуль залишається незмінним) і вектор-функція сталого напряму (змінюється лише модуль).
Якщо в тривимірному евклідовому просторі 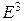 вибрати прямокутну декартову систему координат з ортонормованим базисом
вибрати прямокутну декартову систему координат з ортонормованим базисом 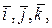 то координати вектор-функції
то координати вектор-функції  будуть скалярними функціями того самого аргументу t:
будуть скалярними функціями того самого аргументу t: 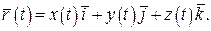 Таким чином, задання вектор-функції рівносильне заданню трьох числових (скалярних) функцій
Таким чином, задання вектор-функції рівносильне заданню трьох числових (скалярних) функцій 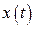 ,
, 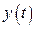 ,
, 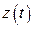 .
.
Якщо вважати 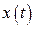 ,
, 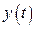 ,
, 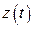 неперервними функціями та інтерпретувати аргумент t як час, то інтуїтивно зрозуміло, що кінець вектора
неперервними функціями та інтерпретувати аргумент t як час, то інтуїтивно зрозуміло, що кінець вектора  , відкладеного від початку кординат, опише криву. Ця крива називається годографом вектор-функції
, відкладеного від початку кординат, опише криву. Ця крива називається годографом вектор-функції  .
.
Для вектор-функції вводяться поняття нескінченно малого вектора, границі, неперервності, похідної, інтеграла, аналогічні відповідним поняттям для скалярної функції.
Нескінченно малим називається вектор 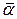 , модуль якого нескінченно малий , модуль якого нескінченно малий 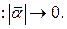
|
Нескінченно малі вектори мають властивості, аналогічні властивостям нескінченно малих скалярних величин:
| 1°. Сума скінченного числа нескінченно малих векторів – нескінченно мала. |
□ Нехай 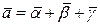 , де
, де 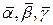 – нескінченно малі вектори.
– нескінченно малі вектори.
Відомо, що 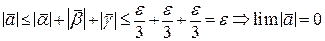 . ■
. ■
| 2°. Якщо вектор є співмножником деякого добутку (скалярного або векторного), один із співмножником якого нескінченно мала величина, а другий – обмежений за абсолютною величиною, то і добуток є нескінченно малою величиною. |
Для нескінченно малих векторів можна ввести поняття порядку малості (порівнюючи їх модулі).
 2015-07-14
2015-07-14 643
643








