Нехай 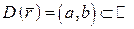 ,
, 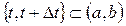 .
.
Нехай вектор-функція  визначена в деякому околі точки визначена в деякому околі точки 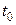 . Похідною векторної функції . Похідною векторної функції 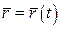 у точці у точці 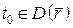 називається границя відношення приросту функції до відповідного приросту аргументу, коли приріст аргументу наближається до 0: називається границя відношення приросту функції до відповідного приросту аргументу, коли приріст аргументу наближається до 0: 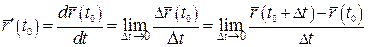 , якщо ця границя існує і скінченна за модулем. , якщо ця границя існує і скінченна за модулем. |
Вектор-функція  , яка має похідну в точці , яка має похідну в точці 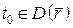 , називається диференційовною в точці t0 . , називається диференційовною в точці t0 . |
З означення границі вектор-функції випливає, що
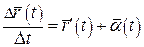 , де
, де 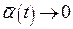 ,
, 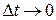 .
.
Отже, приріст диференційовної в точці 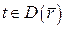 вектор-функції можна подати у виді:
вектор-функції можна подати у виді: 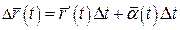 .
.
Звідси випливає, що диференційовна в точці 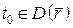 вектор-функція
вектор-функція  є неперервною в цій точці.
є неперервною в цій точці.
Обернене твердження, взагалі кажучи, не є правильним.
Диференціалом векторної функції 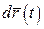 називається головна частина приросту векторної функції: називається головна частина приросту векторної функції: 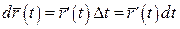 . . |
Властивості диференційовних вектор-функцій:
Теорема 4. Нехай векторні функції 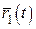 , , 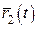 , , 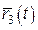 та скалярна функція f(t) визначені на та скалярна функція f(t) визначені на 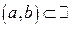 та диференційовні в точці та диференційовні в точці 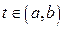 . Тоді в цій точці диференційовні сума та всі можливі добутки їх, причому: 1. . Тоді в цій точці диференційовні сума та всі можливі добутки їх, причому: 1. 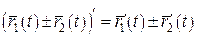 ; 2. ; 2. 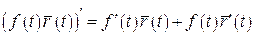 ; 3. ; 3. 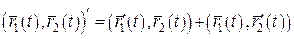 ; 4. ; 4. 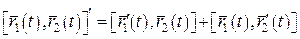 ; 5. ; 5. 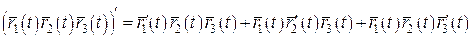 ; 6. ; 6. 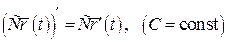 ; 7. ; 7. 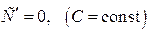 ; 8. ; 8. 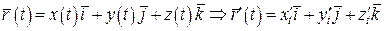 . . |
Для прикладу наведемо доведення твердження 4.
□ Позначимо 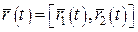 , тоді
, тоді
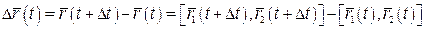 ;
;
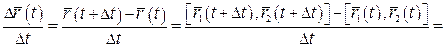
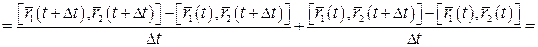
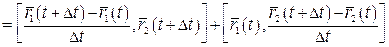 .
.
Скориставшись неперервністю вектор-функції 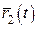 , умовою диференційовності вектор-функцій
, умовою диференційовності вектор-функцій 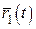 ,
, 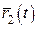 та теоремою 1, перейдемо до границі при
та теоремою 1, перейдемо до границі при 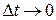 в одержаному співвідношенні. В результаті матимемо:
в одержаному співвідношенні. В результаті матимемо:
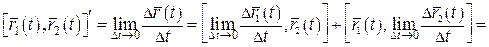
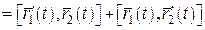 ..■
..■
З теореми 4 випливають відповідні властивості диференціалів вектор-функцій. Наприклад: 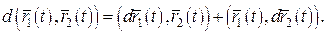
Похідною другого порядку 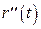 вектор-функції вектор-функції  називається похідна вектор-функції називається похідна вектор-функції 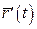 : : 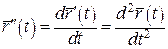 . . |
Аналогічно визначаються похідні вектор-функції вищих порядків.
Регулярною вектор-функцією класу 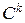 називається вектор-функція, яка на області визначення має неперервні похідні до називається вектор-функція, яка на області визначення має неперервні похідні до 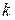 -го порядку включно. Вектор-функція класу -го порядку включно. Вектор-функція класу 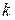 =1 називається гладкою. =1 називається гладкою. |
Позначення: 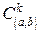 – множина всіх векторних та скалярних функцій, які в кожній точці
– множина всіх векторних та скалярних функцій, які в кожній точці 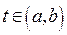 мають неперервні похідні до
мають неперервні похідні до 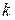 -го порядку включно.
-го порядку включно.
 2015-07-14
2015-07-14 1039
1039








