Як і для скалярної функції, можна дати декілька означень неперервної вектор-функції.
Вектор-функція  називається неперервною в точці називається неперервною в точці 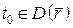 , якщо існує її границя при , якщо існує її границя при 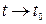 , яка дорівнює значенню векторної функції в цій
точці: , яка дорівнює значенню векторної функції в цій
точці: 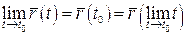 , тобто , тобто
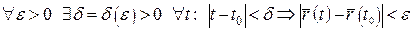 . .
|
Вектор-функція  називається неперервною в точці називається неперервною в точці 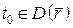 , якщо нескінченно малому приросту аргументу , якщо нескінченно малому приросту аргументу 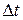 відповідає нескінченно малий приріст вектор-функції відповідає нескінченно малий приріст вектор-функції 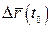 , де , де
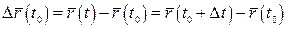 . .
|
Властивості неперервних вектор-функцій:
Теорема 2. Якщо вектор-функції 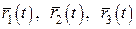 і скалярна функція f(t) визначені на множині U точок прямої і неперервні в точці і скалярна функція f(t) визначені на множині U точок прямої і неперервні в точці 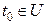 , то в точці , то в точці 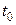 є неперервними їх сума та всі добутки:
1. є неперервними їх сума та всі добутки:
1. 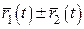 ;
2. ;
2. 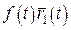 ;
3. ;
3. 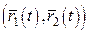 ;
4. ;
4. 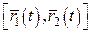 ;
5. ;
5. 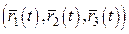 . .
|
Теорема 3.Функція  неперервна в точці неперервна в точці 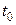 тоді і тільки тоді, коли скалярні функції тоді і тільки тоді, коли скалярні функції 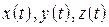 неперервні в цій точці. неперервні в цій точці.
|
| Вектор-функція називається неперервною на множині U,якщо вона неперервна в кожній точці цієї множини. |
 2015-07-14
2015-07-14 412
412








