Вставити пропущені слова так, щоб одержалось правильне твердження

1. Сума ____________числа нескінченно малих векторів є нескінченно малою величиною.

2. Сума нескінченного числа нескінченно малих векторів може не бути ___________________.

3. Якщо вектор є співмножником деякого добутку (скалярного або векторного), один із співмножників якого нескінченно малий, а другий – __________, то і добуток є нескінченно малою величиною.

4. Якщо один із співмножників деякого добутку є нескінченно малою величиною, а другий – обмеженою величиною, то добуток є _____________.

5. Границею вектор-функції називається __________ вектор 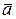, такий що різниця 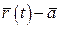є ____________________.

6. Вектор-функція називається неперервною в точці її області визначення, якщо нескінченно малому приросту ___________відповідає нескінченно малий приріст _____________.

7. Вектор-функція називається ____________ в точці 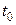, якщо існує її границя при 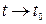, причому .

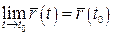8. Вектор-функція називається неперервною на відрізку, якщо __________.

9. Похідною векторної функції 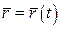у точці 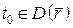називається ____________ границя відношення приросту _________ до відповідного приросту ____________, коли цей приріст наближається до ___.

10. Вектор-функція називається диференційовною в точці t₀ , якщо вона має _____________ в точці .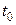

11. Диференціал векторної функції 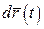є ___________частиною приросту векторної функції.

12. Вектор-функція, яка на області визначення має неперервну похідну першого порядку називається _________.

13. Вектор-функцією класу 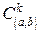називається функція, яка на інтервалі 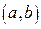має ____________ похідні до _____ порядку _______.

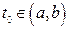14. Аналітичною вектор-функцією у точці називається функція, яка має у цій точці похідні ___________порядку та існує окіл точки t₀,в якому ряд Тейлора збігається до функції .

15. Невизначеним інтегралом від вектор-функції називається вектор-функція, ________________ якої дорівнює ____________.