1. Из всей совокупности спаренных частичных отрезков, образующих сетку 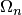 , по заданной величине
, по заданной величине 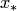 выбрать два пересекающихся "окна"
выбрать два пересекающихся "окна" 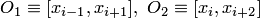 (предполагается, что
(предполагается, что 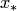 принадлежит внутреннему отрезку
принадлежит внутреннему отрезку 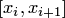 ).
).
2. Для "окон" 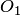 и
и 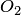 вычислить значения коэффициентов Лагранжа: — для "окна"
вычислить значения коэффициентов Лагранжа: — для "окна" 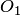 и — для "окна"
и — для "окна" 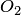 . Путем суммирования проверить правильность полученных значений коэффициентов:
. Путем суммирования проверить правильность полученных значений коэффициентов:
3. Используя значения коэффициентов Лагранжа, вычислить значения 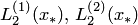 по формуле (4.14).
по формуле (4.14).
Если в расчетах не требуется высокая точность интерполирования, то можно ограничиться выбором одного "окна", например 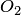 , и тогда
, и тогда 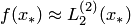 . Для достижения повышенной точности интерполяцию провести для двух "окон" и результаты
. Для достижения повышенной точности интерполяцию провести для двух "окон" и результаты 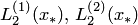 усреднить:
усреднить:
При этом порядок интерполяции повышается на единицу, т.е. 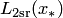 аппроксимирует точное значение с четвертым порядком, поскольку погрешность составляет величину
аппроксимирует точное значение с четвертым порядком, поскольку погрешность составляет величину 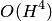 , где
, где 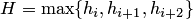 .
.
Замечание. Если 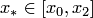 или
или 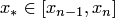 , то выбирается одно "окно"
, то выбирается одно "окно" 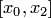 или
или 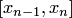 соответственно.
соответственно.
Геометрическая интерпретация параболической интерполяции изображена на рис. 4.4. Параболе 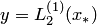 соответствует кривая
соответствует кривая 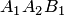 , параболе
, параболе 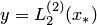 — кривая
— кривая 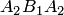 . Точка
. Точка 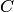 соответствует значению
соответствует значению 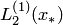 , точка
, точка 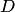 — значению
— значению 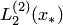 точка
точка 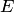 — значению
— значению 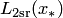 .
.
Приведем оценки погрешностей линейной и параболической интерполяции. Вначале предположим, что сетка 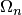 равномерная (это имеет значение только для параболической интерполяции). Формулы (4.13), (4.14) и оценки (4.22), записанные для "окон" интерполяции, упрощаются, если ввести в рассмотрение новую переменную — фазу интерполяции и
равномерная (это имеет значение только для параболической интерполяции). Формулы (4.13), (4.14) и оценки (4.22), записанные для "окон" интерполяции, упрощаются, если ввести в рассмотрение новую переменную — фазу интерполяции и 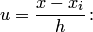
Здесь учтено, что 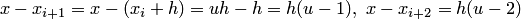 . Очевидно, что для
. Очевидно, что для 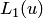 величина
величина 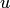 изменяется в диапазоне
изменяется в диапазоне 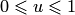 , а для
, а для 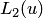 — в диапазоне
— в диапазоне 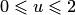 . Для получения мажорант в оценке (4.22) необходимо найти
. Для получения мажорант в оценке (4.22) необходимо найти 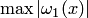 и
и 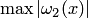 . Преобразуя зависимости
. Преобразуя зависимости 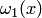 и
и 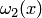 к новой переменной
к новой переменной 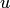 , получаем
, получаем 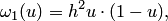
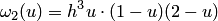 и находим максимумы:
и находим максимумы:
Таким образом, реализуются следующие оценки погрешностей линейной и параболической интерполяции, справедливых для соответствующих "окон":
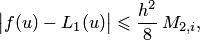
| (4.23) |
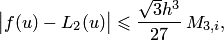
| (4.24) |
где. При этом предполагается, что 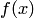 принадлежит классам функций
принадлежит классам функций  соответственно для линейной и параболической интерполяции. Таким образом, из оценок (4.23), (4.24) следует, что линейная интерполяция обеспечивает на частичном отрезке
соответственно для линейной и параболической интерполяции. Таким образом, из оценок (4.23), (4.24) следует, что линейная интерполяция обеспечивает на частичном отрезке 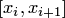 второй порядок аппроксимации или погрешности по
второй порядок аппроксимации или погрешности по 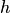 , а параболическая (без осреднения) на двойном отрезке
, а параболическая (без осреднения) на двойном отрезке  — третий порядок. Данные пофешности, как отмечалось во введении и предыдущих разделах, сокращенно записываются как
— третий порядок. Данные пофешности, как отмечалось во введении и предыдущих разделах, сокращенно записываются как 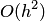 и
и 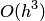 . При реализации алгоритма с осреднением порядок параболической интерполяции становится равным
. При реализации алгоритма с осреднением порядок параболической интерполяции становится равным 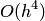 .
.
 2015-07-14
2015-07-14 945
945








