Лабораторная работа № 3
Решение задач оптимизации с помощью надстройки «Поиск решения» MS Excel
Цель работы
Построить математическую модель задачи линейного программирования и найти оптимальное решение с помощью надстройки «Поиск решения» MS Excel.
Пример. Производство двух видов изделий А и В осуществляется на четырёх станках. Время обработки (в часах) каждого изделия на каждом станке приводится в таблице.
| Вид изделия | Время обработки одного изделия на станке | |||
| I | II | III | IV | |
| А | ||||
| В |
Сколько изделий каждого вида должно произвести предприятие, чтобы получить максимальный доход, если станки можно использовать в течении 12, 10, 18, 28 часов, а доход от реализации изделия А – 2 руб., изделия Б – 3 руб.?
Исходя из условия задачи, целевая функция будет иметь вид:
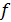 (x) = 2
(x) = 2 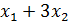
 max
max
Значения параметров должны удовлетворять следующим ограничениям:
 ≤ 12
≤ 12
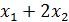 ≤
≤ 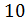
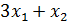 ≤
≤ 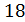
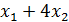 ≤ 2
≤ 2 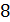
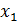
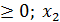
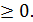
Решим задачу линейного программирования с помощью возможностей табличного процессора MS Excel.
1. Запускаем MS Excel.
2. На Листе текущей Книги в ячейки 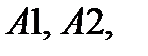 зарезервированные для управляемых переменных
зарезервированные для управляемых переменных 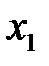 ,
, 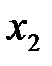 , соответственно, введём любые начальные значения. Пусть это будет
, соответственно, введём любые начальные значения. Пусть это будет 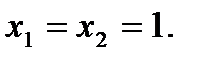
3. В ячейку  введём формулу
введём формулу 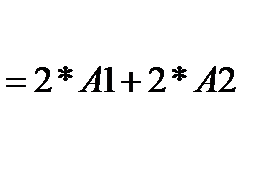
4. В ячейку  формулу
формулу 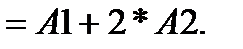
5. В ячейку 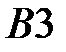 формулу
формулу 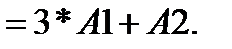
6. В ячейку 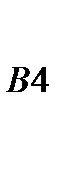 формулу
формулу 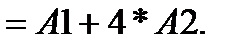
7. В ячейку 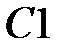 формулу =
формулу = 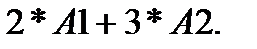
8. Запускаем режим «Поиск решения» (Меню: Данные  Поиск решения).
Поиск решения).
9. В появившемся диалоговом окне введём информацию:
· Установить целевую ячейку: 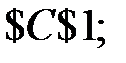
· Равной: максимальному значению;
· Изменяя ячейки: 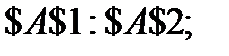
· Ограничения: 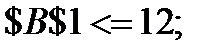
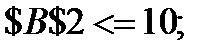
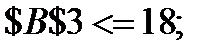
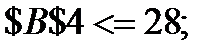
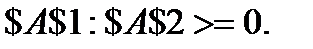
10. Нажимаем кнопку «Выполнить».
Рассмотрим другой способ решения с помощью табличного процессора MS Excel.
Пример. Предприятие может работать по двум технологическим процессам, причем за единицу времени по 1-й технологии выпускает 260 изделий, по 2-й — 300 изделий. В таблице указаны затраты каждого ресурса в единицу времени.
| Ресурсы | Технологический процесс | Объем ресурса | |
| Сырье | |||
| Электроэнергия | 0,2 | 0,4 | |
| Накладные расходы | |||
| Зарплата, ден. ед. |
Найти план максимального выпуска продукции из имеющихся ресурсов.
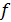 (x) =
(x) = 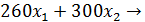 max
max
16 x 1 + 12 x 2 ≤ 1200
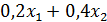
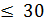
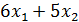
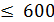
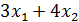
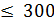
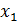
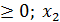
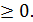
| А | В | С | D | E | F | G | ||
| Производственный план | ||||||||
| Переменные | X1 | Х2 | ||||||
| Значения | ||||||||
| Коэф. в ЦФ | С1 | С2 | ||||||
| Значения | Целевая функция | =СУММПРОИЗВ (В7:С7; $В$4:$С$4) | ||||||
| Ресурсы | Расход ресурсов | Лев. часть | Огра- нич. | Прав. часть | Разница | |||
| Сырье | =СУММПРОИЗВ (В11:С11; $В$4:$С$4) | <= | =F11-D11 | |||||
| Электроэнергия | 0,2 | 0,4 | =СУММПРОИЗВ (В12:С12; $В$4:$С$4) | <= | =F12-D12 | |||
| Накл. расходы | =СУММПРОИЗВ (В13:С13; $В$4:$С$4) | <= | =F13-D13 | |||||
| Зарплата | =СУММПРОИЗВ (В14:С14; $В$4:$С$4) | <= | =F14-D14 | |||||
1. В ячейки B7, C7 введём коэффициенты целевой функции;
2. В ячейки B11:B14, C11:C14, E11:E14 введём коэффициенты, а также знаки оганичений, соответствующие условию задачи, как это показано в таблице;
3. В ячейки D11:D14 введём формулы из таблицы, соответствующие левым частям ограничений;
4. В ячейки F11:F14 введём формулы разности правых и левых частей ограничений (остаток ресурсов);
5. В ячейку G7 введём формулу для вычисления значения целевой функции: =СУММПРОИЗВ(B7:C7;$B$4:$C$4);
6. Запускаем режим «Поиск решения»;
7. В появившемся диалоговом окне введём информацию:
· Установить целевую ячейку: 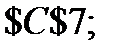
· Равной: максимальному значению;
· Изменяя ячейки: 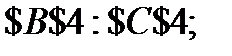
· Ограничения: 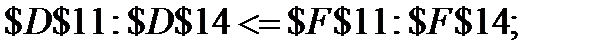
8. Нажимаем кнопку «Выполнить».
Результат решения:
| А | В | С | D | Е | F | G | ||
| Производственный план | ||||||||
| Переменные | X1 | Х2 | ||||||
| Значения | 42,85714 | 42,85714 | ||||||
| Коэфф. в ЦФ | С1 | С2 | ||||||
| Значения | Целевая функция | |||||||
| Ресурсы | Расход ресурсов | Лев. часть | Огра- нич. | Прав, часть | Разница | |||
| Сырье | <= | |||||||
| Электроэнергия | 0,2 | 0,4 | 25,71429 | <= | 4,285714 | |||
| Накл. расходы | 471,4286 | <= | 128,5714 | |||||
| Зарплата | <= | |||||||
Варианты заданий:
Вариант 1.
Фабрика выпускает три вида тканей. Суточные ресурсы фабрики следующие: 780 единиц производственного оборудования; 850 единиц сырья; 790 единиц электроэнергии, расход которых на единицу сырья представлен в таблице:
| Ресурсы | Ткани | ||
| I | II | III | |
| Оборудование | |||
| Сырьё | |||
| Электроэнергия |
Цена 1м I ткани 8 руб.; II – 7 руб.; III – 6 руб. Сколько надо произвести ткани, чтобы получить максимальный доход?
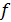 (x) =8
(x) =8 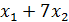 +
+ 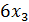
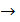 max
max
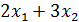 +
+ 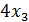
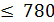
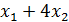 +
+ 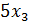
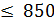
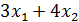 +
+ 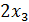
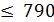
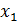
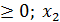
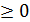 ;
; 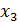
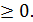
Вариант 2.
Требуется составить смесь, содержащую три химических вещества А, В, С. Известно, что составленная смесь должна содержать вещества А не менее 6 единиц, вещества В не менее 8 единиц, вещества С не менее 12 единиц. Вещества А, В, С содержатся в трёх видах продукции I, II, III в концентрации, указанной в таблице.
| Продукты | Химические вещества | ||
| А | В | С | |
| I | |||
| II | |||
| III |
Стоимость единицы продуктов I, II, III, различна, единица продута I стоит 2 руб., II – 3 руб., III – 2,5 руб. Смесь составить так, чтобы стоимость используемых продуктов была наименьшей.
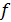 (x) =2
(x) =2 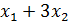 +
+ 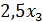
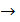 min
min
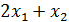 +
+ 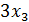
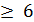
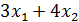 +
+ 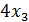
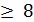
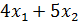 +
+ 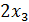
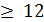
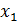
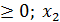
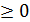 ;
; 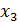
Вариант 3.
Для изготовления трёх видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цена каждого продукта приведены в таблице.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | ||
| А | В | С | ||
| I | ||||
| II | ||||
| III | ||||
| Цена изделия (ден. ед.) |
Определить, сколько изделий каждого вида нужно произвести, чтобы стоимость изготовления продукции была максимальной.
Вариант 4.
Для изготовления двух видов тары (бочек и ящиков) употребляют два вида древесины. Расход древесины каждого вида на каждое изделие, объём ресурсов и прибыль на единицу изделия даны в таблице.
| Изделия | Расход древесины в 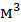 | Прибыль на единицу продукции (ден. ед.) | |
| I | II | ||
| Бочки | 0,15 | 0,2 | 1,5 |
| Ящики | 0,2 | 0,1 | 1,2 |
Объём ресурсов, 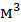 |
Определить, сколько ящиков и бочек должен изготовить завод, чтобы прибыль была максимальной.
Вариант 5.
Фабрика производит ткань двух сортов. В таблице указаны нормы расхода ресурсов на 1 тыс. м ткани и объём ресурсов. Найти план выпуска ткани, максимизирующий её стоимость.
| Виды ресурсов | Объём ресурсов (тыс.) | Нормы расхода | |
| I | II | ||
| Станки, ст.-час | |||
| Пряжа, кг | |||
| Красители, кг | 0,5 | ||
| Цена, ден. ед. |
Вариант 6.
Для производства двух типов изделий А и В используется три типа оборудования. В таблице дано время изготовления единицы изделия (в часах), ресурсы времени использования каждого типа оборудования, прибыль от реализации единицы изделий каждого вида. Составить план производства, максимизирующий прибыль от реализации продукции.
| Тип оборудования | Изделия | Ресурсы времени | |
| А | В | ||
| I | |||
| II | |||
| III | |||
| Прибыль (ден. ед.) |
Вариант 7.
На швейной фабрике для изготовления четырёх видов изделий может быть использована ткань трёх артикулов. Нормы расхода ткани всех артикулов на пошив одного изделия, а так же имеющееся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия каждого вида приведены в таблице.
| Артикул ткани | Нормы расхода ткани (м) на одно изделие вида | Общее коли- чество ткани | |||
| I | - | ||||
| II | - | ||||
| III | - | ||||
| Цена одного из- делия (ден. ед.) |
Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовления продукции была максимальной.
Вариант 8.
Для изготовления трех видов изделий А, В, С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия данного вида.
Требуется определить, сколько и какого вида изделий следует изготовить предприятию, чтобы прибыль от их реализации была максимальной.
| Тип оборудования | Затраты времени (станко~ч) на обработку одного изделия вида | Общий фонд рабочего времени оборудования (ч) | ||
| А | В | С | ||
| Фрезерное | ||||
| Токарное | ||||
| Сварочное | ||||
| Шлифовальное | ||||
| Прибыль |
Вариант 9.
Кондитерская фабрика для производства трех видов карамели А, В, С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство 1 т карамели данного вида приведены в таблице. В ней же указано общее количество сырья каждого вида, которое может быть использовано фабрикой, а также приведена прибыль от реализации 1 т карамели данного вида.
| Вид сырья | Нормы расхода сырья (т) на 1 т карамели | Общее количество сырья (т) | ||
| А | В | С | ||
| Сахарный песок | 0,8 | 0,5 | 0,6 | |
| Патока | 0,4 | 0,4 | 0,3 | |
| Фруктовое пюре | - | 0,1 | 0,1 | |
| Прибыль от реализации 1 т продукции (руб.) |
Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации.
Вариант 10.
Компания производит полки двух размеров – А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В – 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин. машинного времени, а для изготовления одной полки типа В - 30 мин. ЭВМ можно использовать 160 ч в неделю. Если прибыль от продажи полок типа А составляет 3 дол., а от полок типа В - 4 дол., то сколько полок каждого типа следует выпускать в неделю.
Вариант 11.
Фирма занимается составлением диеты, содержащей, по крайней мере, 20 единиц белков, 30 единиц углеводов, 10 единиц жиров и 40 единиц витаминов. Как дешевле всего достичь этого при указанных в таблице ценах на 1 кг (или 1 л) пяти имеющихся продуктов?
| Хлеб | Соя | Сушеная рыба | Фрукты | Молоко | |
| Белки | 2 | 2 | |||
| Углеводы | |||||
| Жиры | |||||
| Витамины | |||||
| Цена |
Вариант 12.
Небольшая фирма производит два вида продукции, столы и стулья. Для изготовления одного стула требуется 3 фута древесины, а для изготовления одного стола - 7 футов. На изготовление одного стула уходит 2 ч. рабочего времени, а на изготовление стола - 8 ч. Каждый стул приносит 1 дол. прибыли, а каждый стол - 3 дол. Сколько стульев и сколько столов должна изготовить эта фирма, если она располагает 420 футами древесины и 400 ч. рабочего времени и хочет получить максимальную прибыль?
Вариант 13.
Фирма, изготовляющая деревянную продукцию, производит два вида обшивочных панелей: колониальную и западную. Производство панелей осуществляется двумя операциями: прессованием и отделкой. Задача администрации фирмы - узнать, сколько пластов обоих типов обшивочной панели нужно производить в месяц, чтобы получить максимальную прибыль.
Проблема в том, что продукция панелей ограничена - фирма ограничена средствами для производства продуктов. Задача состоит в оптимальном размещении средств для получения наибольшей прибыли.
Фирма обладает ресурсами в условиях доступности леса, имеется достаточно рабочих часов для прессования и обработки, а также долларовый бюджет.
Ресурсные потребности и возможности для каждого типа панелей, которые образовывают параметры модели, представлены в таблице.
| Необходимые средства для партии из 100 пластов обшивочной панели | Всего средств в месяц | ||
| Средства | Колониальные | Западные | |
| Деревянная продукция | 20 кг | 40 кг | 4000 кг |
| Прессование | 4 ч | 6ч | 900 ч |
| Отделка | 4 ч | 4 ч | 600 ч |
| Стоимость | $30 | $50 | $6000 |
Фирма получает 80 дол. прибыли за каждые 100 пластов колониальной панели и 100 дол. - за каждые 100 пластов западной панели.
 2015-07-21
2015-07-21 5077
5077