Выделим внутри диэлектрика некоторый объем V, ограниченный поверхностью S. Подсчитаем, сколько заряда проходит через элемент dS воображаемой поверхности, когда материал поляризуется. При появлении электрического поля положительные заряды молекул сместятся на некоторое расстояниевдоль поля, а отрицательные - в противоположном направлении. При этом каждая молекула приобретет дипольный момент, определяемый соотношением (5.3), причем вектор смещения будет направлен вдоль поля, а средняя длина вектора смещения l для диполей, находящихся в прилегающем к dS слою, будет согласно (5.4) связана с поляризацией этого слоя соотношением
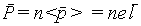 | (5.7) |
откуда l = P / ne.
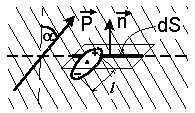 Рис. 5.3 Рис. 5.3 | Элемент поверхности dS пересечет все те диполи, центры которых расположены в прилегающем к нему слое толщины l |cos α|, где α - угол между нормалью к dS и направлением вектора поляризованности (рис. 5.3). Объем этого слоя равен l |cos α| dS, а число пересекаемых элементом dS диполей равно n l |cos α| dS. |
Следовательно, для выбранного элемента поверхности соответствующая абсолютная величина нескомпенсированного заряда внутри объема V равна
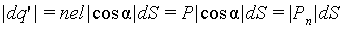 | (5.8) |
При этом, если cos α > 0, то снаружи от элемента dS находятся положительные заряды, а внутри - отрицательные, а если cos α < 0, то - наоборот.
Таким образом алгебраическая величина нескомпенсированного заряда внутри объема V равна dq' = -Pn dS = - P d S. Тогда поток вектора P через поверхность S, ограничивающую объем V,связан с полным связанным зарядом q ' в объеме соотношением
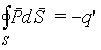 | (5.9) |
Последнее соотношение представляет собой теорему Гаусса для вектора P.
Преобразуем левую часть выражения (5.9) по теореме Остроградского-Гаусса, а связанный заряд q' представим, как
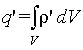 | (5.10) |
где ρ' - объемная плотность связанного заряда.
Тогда будем иметь
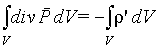 | (5.11) |
откуда с учетом произвольности выбранного объема V получим теорему Гаусса для вектора поляризованности в дифференциальной форме:
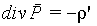 | (5.12) |
Выясним, в каких случаях объемная плотность связанных зарядов отлична от нуля. Выразим P в (5.12) через E согласно (5.6)
| ρ' = –∇(κεoE)= –εo∇(κE) = –εo(E∇κ+κ∇E) | (5.13) |
В теореме Гаусса для вектора E, записанной в дифференциальной форме (2.17), в правой части стоит объемная плотность заряда, включающая в случае диэлектрика как плотность сторонних, так и связанных зарядов
| ∇E=(ρ+ρ')/εo | (5.14) |
Заменяя в (5.13) ∇ E согласно (5.14) получим
| ρ' = –εoE∇κ – κρ –κρ' | (5.15) |
Отсюда
| ρ' = – (εoE∇κ + κρ)/(1+κ) | (5.16) |
Из последнего выражения видно, что объемная плотность связанного заряда в диэлектрике отлична от нуля в двух случаях: (1) когда диэлектрик поляризуется неоднородно (κ есть функция координаты) и/или (2) в диэлектрике присутствует сторонний заряд (ρ отлично от нуля). При однородной поляризации и отсутствии стороннего заряда внутри диэлектрика равенство нулю связанного объемного заряда легко усматривается из рис. 5.1.
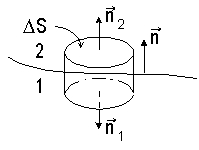 Рис. 5.4 Рис. 5.4 | Рассмотрим границу раздела двух однородных изотропных диэлектриков 1 и 2 (рис. 5.4). Выделим мысленно на границе раздела цилиндр с площадью основания Δ S с образующей, перпендикулярной границе раздела. Выберем произвольно направление нормали nк границе,как показано на рисунке. Пусть площадка Δ S, вырезаемая цилиндром на границе,столь мала, что ее можно считать плоской, а поляризованность каждого из диэлектриков в ее пределах постоянной. |
Найдем поток Ф вектора P через поверхность цилиндра. Поток через нижнее основание цилиндра равен P 1·Δ S cos (P 1, n 1), а через верхнее P 2·Δ S cos (P 2, n 2), где индексами 1 и 2 обозначены величины, относящиеся соответственно к внутренней и внешней по отношению к нормали n сторонам границы раздела. Поток через боковую поверхность цилиндра обозначим Ф'. Тогда будем иметь
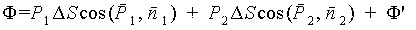 | (5.17) |
Направление нормали n 2 совпадает с направлением нормали n, а направление нормали n 1прямо противоположно. Следовательно
| P 1·Δ S cos (P1,n1) = - P 1 n ; | P 2·Δ S cos (P2,n2)= P 2 n , |
где P 1 n и P 2 n - проекции вектров P 1и P 2 на нормаль n. Таким образом
Ф= (P 2 n - P 1 n ) Δ S + Ф'.
Будем теперь уменьшать высоту цилиндра, не изменяя при этом его основания. Поток Ф' через безгранично уменьшающуюся боковую поверхность будет стремиться к нулю, так что общий поток через поверхность цилиндра сведется в пределе к потоку через его основания:
Ф= (P 2 n - P 1 n ) Δ S.
Для однородных диэлектриков объемный связанный заряд, как было показано выше, равен нулю. Стало быть внутри цилиндра окажется заряд, расположенный на границе раздела на элементе поверхности Δ S. Этот заряд равен Δ S ·σ', где σ' - поверхностная плотность связанного заряда на границе раздела диэлектриков. На основании теоремы Гаусса для вектора P запишем
(P 2 n - P 1 n ) Δ S = -Δ S ·σ',
откуда
| (P 2 n - P 1 n ) = - σ' | (5.18) |
Иными словами, на границе раздела нормальная составляющая вектора P испытывает разрыв, величина которого зависит от σ'. В частности, если среда 2 вакуум, то P 2 n = 0 и
| Pn = σ' | (5.19) |
где Pn проекция вектора P на внешнюю нормаль к поверхности данного диэлектрика.
 2015-07-21
2015-07-21 4071
4071
