Заняття 34-35

Тема 10.4. Невластиві інтеграли по нескінченних проміжках. Невластиві інтеграли від функцій з особливостями в точках відрізку інтегрування. Умови збіжності.

ВПРАВИ

1. Дослідити збіжність невласних інтегралів.

а) .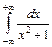

Розв'язання. = .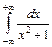

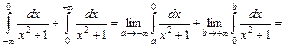
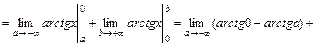
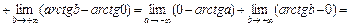
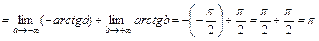Даний невласний інтеграл збігається.

Відповідь: .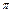

б) .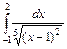

Розв'язання. Підінтегральна функція має незкінчений розрив в точці x = 1. Ця точка лежить усередині відрізка інтегрування [-1; 2]. Тому

.

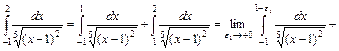
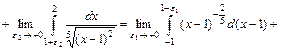
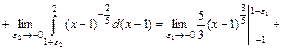
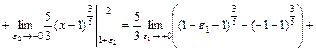
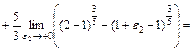
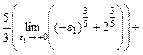
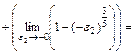
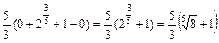Даний невласний інтеграл збігається.

Відповідь: .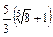

2. Дослідити на збіжність невластивий інтеграл .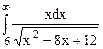

Розв’язання. Підінтегральна функція необмежена в околах точок х=2, х=6. Точка х=6 належить проміжку інтегрування. Даний інтеграл невластивий з двома особливостями: нескінченною границею і особливою точкою. Розбиваємо його на два інтеграла, кожний з яких має одну особливість:

= + .

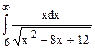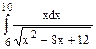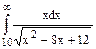Знайдемо первісну підінтегральної функції: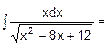

= = =

= = .

= =

=

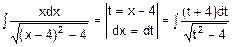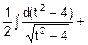
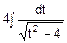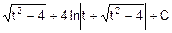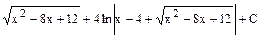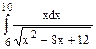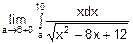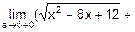
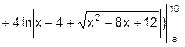
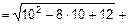
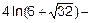
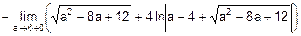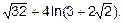
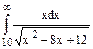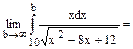
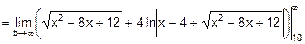= =¥- інтеграл розбіжний. Відповідь: даний інтеграл розбіжний.