Тема 11.1 Задачі, що приводять до кратних інтегралів. Обчислення кратних інтегралів по клітинах та по правильних областях.
1. Обчислити подвiйний iнтеграл 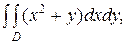
де D – область, обмежена параболами: y=x2 i y2=x.
Розв`язання. Побудуємо область iнтегрування:
Для знаходження координат точек перетину


 розв`яжемо систему рiвнянь:
розв`яжемо систему рiвнянь:
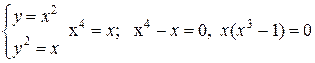


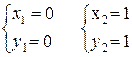
Обчислимо iнтеграл, виконавши внутрiшнє
iнтегрування по y, а зовнiшнє по х.
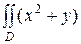 dxdy =
dxdy = 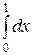
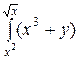 dy =
dy = 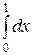 [x2y+y2/2]
[x2y+y2/2] 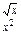
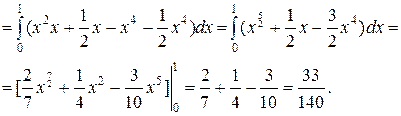
2. Обчислити потрiйний iнтеграл 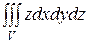 , якщо область
, якщо область
обмежена площинами x=0,y=0,x+y+z=1.
Розв`язання.
Побудуємо область iнтегрування.
Область обмежена зверху площиною
z=1-х-y, а знизу площиною z=0.
Проекцiєю на площину xoy служить
трикутник, створений прямими
x=0, y=0, y=1-x.
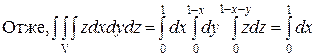 =
=
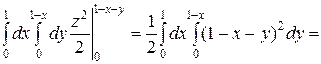
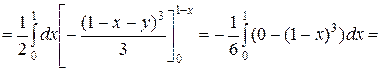
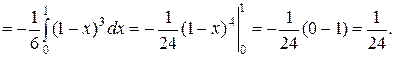
3. Змiнити порядок iнтегрування в iнтегралi:
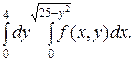
Розв`язання.
Область iнтегрування обмежена лiнiями y=0,y=4,x=0,
x= 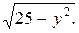
Замiнимо порядок iнтегрувння,
для чого область D розiб`ємо на
двi областi D1 i D2. Область D1
обмежена лiнiями: x=0,x=3,y=0,
y=4. Область Д2 обмежена лiнiя-
ми: x=3,x=5.y=0,x=25-x2.
Тодi: 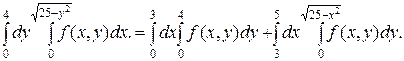
 2015-08-21
2015-08-21 540
540








