Вариационные задачи с подвижными границами. Пример в теории управления

Задан функционал 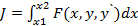, но крайние точки не закреплены.

Вместо точек заданы 2е кривые

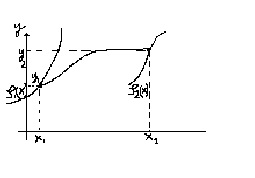
Условие оптимума: главная линейная часть приращения равна 0. Предположим, что мы нашли решение, следовательно знаем точки (x₁,y₁), (x₂,y₂) и минимизировали функционал.

Функция, удовлетворяющая уравнению Эйлера –экстремальная. Решение задачи с подвижными границами может достигаться на экстремалях.

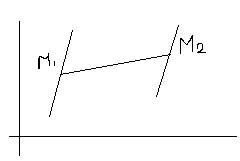Рассмотрим пример

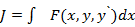
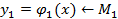
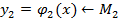
Задача

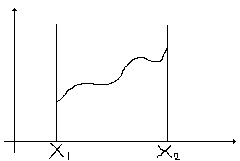
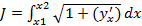
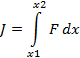
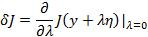
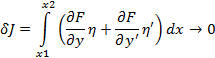
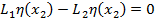при 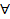вещественных аргументах.

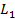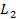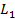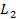Лин. Форма принимает 0е значения только когда и =0 получаем условие =0 =0

Т.е. на концах должны выполняться условия:

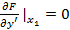
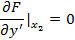
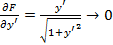это даёт условие, что производные:

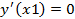
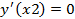
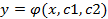
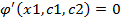
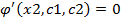система уравнений

Уравнение экстремали для: :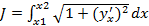

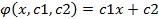
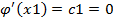
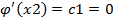
1. Обращение к уравнению Эйлера и нахождение уравнения Экстремали.

2. Условие трансверсальности-условие вхождения экстремали в границу для поиска констант с1 и с2