Пример использования уравнения Эйлера для поиска оптимального управления

Задача. Найти оптимальную (кратчайшую) кривую между двумя точками.

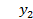dy

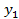dx

;

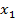
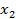
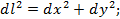
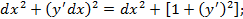
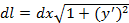Функционал: 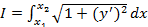, где .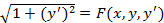

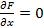
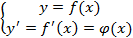
Первое правило дифференцирования: речь идет только о вещественных аргументах. Запишем:

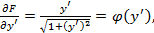
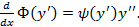
Теперь мы можем записать уравнение Эйлера: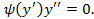

Решение: рассмотрим первый случай.

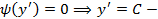общий вид решения.

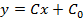– семейство прямых.

Второй случай.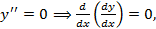

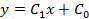- общее решение (все прямые).

Итак, оптимальная траектория – прямая, соединяющая эти две точки.

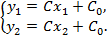– система линейных уравнений относительно констант.

Итак, общий алгоритм решения такой задачи (задачи Эйлера).

1. Составить уравнение Эйлера (два правила дифференцирования);

2. Найти общее решение уравнений Эйлера: 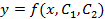, т.к. второй порядок.

3. Определить константы интегрирования из условий: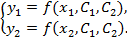

Всякая задача должна быть поставлена корректно:

1. Существование решения;

2. Единственность решения;

3. Решения должны быть устойчивы по отношению к некоторым изменениям в установке.