2015-08-21
990
При решении вариационной задачи на условный экстремум (см. вопрос 13) удобно использовать метод множителей Лагранжа, сохраняющий полное равноправие переменных, т.е. сведение задачи к задаче на безусловный экстремум. Дан функционал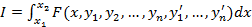 
При наличии условий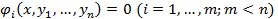 
Запишем функцию Лагранжа Ф:
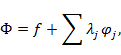
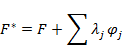
Составим функционал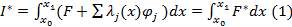 
, который исследуется на безусловный экстремум, т.е. решается система уравнений Эйлера
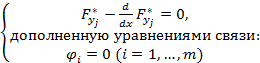(2)
Однако, остается невыясненным, всегда ли можно применить этот метод. Поэтому ограничимся формулировкой теоремы:
Теорема. Функции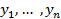 
, реализующие экстремум функционала 
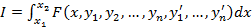при наличии условий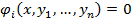 
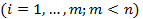удовлетворяют при соответствующем выборе множителей Лагранжа 
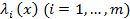уравнениям Эйлера, составленным для функционала (1). Функции 
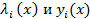определяются из системы (2).
