2015-08-21
552
Переход к дискретной системе: рассмотрим U,x в отдельных точках.
Будем искать приближенное значение U,x на интервалах
, 
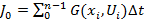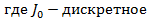
Рассм.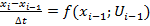 
– дифур. стало разностным уравнением
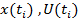– дискретная задача
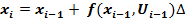– ограничение
Метод динамического программирования – метод поиска наибольшего/наименьшего значения ф-ции многих переменных при наличии ограничения на переменные, ограничения в виде разностных уравнений.
Если ограничение общего вида, то этот метод не подходит.
Вместо сложной задачи решаем много простых задач поиска наиб./наим. значения ф-ции одного аргумента.Например необходимо найти методом градиента наиб./наим. значение.Задача общая, общего решения нет … Наш метод опред. решение.
Решение задачи начинается с конца траектории (с конечной точки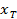 
)
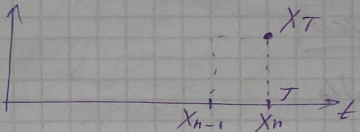Решение основано на принципе оптимальности
Шаг 1 для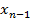 
. Пусть 
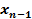- известно. Тогда 
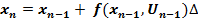-разностное уравнение. Для каждого 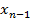находим оптимальное значение 
.
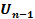Уравнение становится относительно корней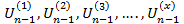 
- необходимо выбрать оптимальное уравнение: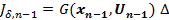 
Итоги шагов: Шаг 1 для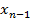
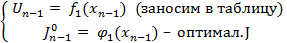
Шаг 2 для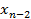 
. Пусть 
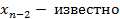.Тогда 
.
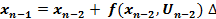Дискретный критерий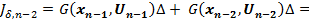 
начиная с 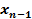движемся оптимально 
+ 
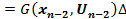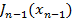.Из 4-ёх аргументов получили 3.
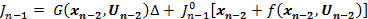
Шаг 2 для 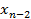. ИТОГ: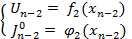 
Далее доходим до шага, где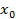 
-известно, потом пойдем в обратном направлении
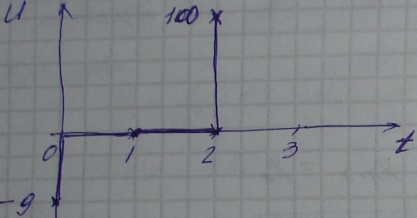
ПРИМЕР: 10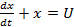 
x(0) =1, x(T) =10 T=3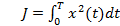 
Оптимальным способом перевести систему из нач. сост. в конечное за 3 секунды, чтобы критерий принял минимальное значение. Принять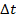 
=1. Разностное уравнение:
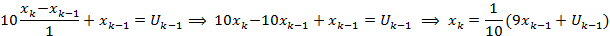
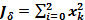
Шаг 1. Для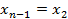 
. Пусть 
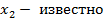. Разн. уравнение:
, 
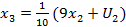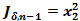. Найти оптимальное управляющее воздействие:
x(T) =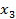 
=10 
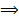
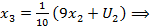
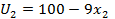Итог: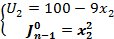 
Шаг 2. Для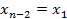 
. Пусть 
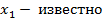. Разн. уравнение:
, 
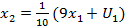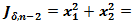начиная с 
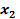движение оптимально =
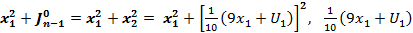-приравниваем к 0 
Итог: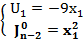 
Шаг 3. Для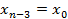 
. Пусть 
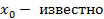. Разн. уравнение:
, 
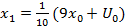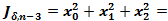начиная с 
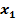движение оптимально =
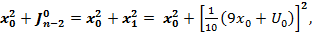Ищем оптим. 
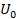для каждого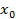 
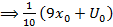-приравниваем к 0 .Итог: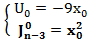 
Движемся в обратную сторону: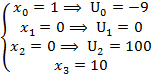 
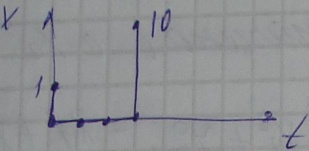
Для непрерывных систем: 
- 
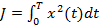
Для диф-я 2-го порядка решение усложняется. Метод динамического программирования применим в комбинаторных задачах.
