Пусть объект управления описывается системой уравнений 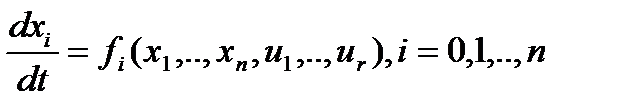 .или в векторной форме
.или в векторной форме 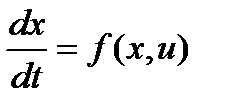 ,где
,где 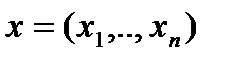 -вектор координат состояния,
-вектор координат состояния, 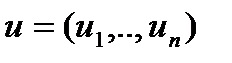 -вектор координат управления. Основная задача оптимального управления: среди всех допустимых управлений, переводящих динам. Сис-му из начального положения x0 в конечное x1, найти оптимальное. Для определения критерия оптимальности рассмотрим функционал
-вектор координат управления. Основная задача оптимального управления: среди всех допустимых управлений, переводящих динам. Сис-му из начального положения x0 в конечное x1, найти оптимальное. Для определения критерия оптимальности рассмотрим функционал 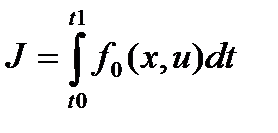 .Он должен достигать минимума.
.Он должен достигать минимума.
Принцип максимума Понтрягина основан на установлении связи оптимизируемого функционала J с динамикой процесса. Эта связь устанавливается через функцию Гамильтона 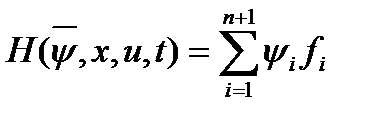 ,где
,где 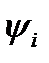 удовлетворяет уравнениям
удовлетворяет уравнениям 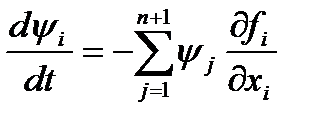 ,j=0,1,..,n. Принцип максимума Понтрягина состоит в том, что для оптимального управления и соответствующих координат
,j=0,1,..,n. Принцип максимума Понтрягина состоит в том, что для оптимального управления и соответствующих координат 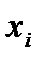 ,для которых критерий J имеет минимальное значение, функция Гамильтона H имеет максимум(по аргументу U).
,для которых критерий J имеет минимальное значение, функция Гамильтона H имеет максимум(по аргументу U).
Функции H(y, x, и) ставится в соответствие каноническая (гамильтонова) система (относительно y, х) 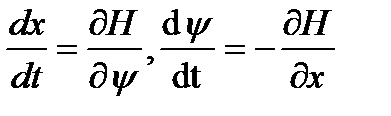 .
.
 2015-08-21
2015-08-21 471
471








