Понятие функции комплексного переменного

Определение Пусть G область в комплексной плоскости C. Если каждой точке 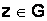поставить в соответствие единственное комплексное число 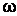, то говорят, что на области 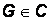задана однозначная функция комплексного переменного и обозначается 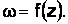Область G называется областью определения функции, z – аргумент функции, 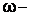значение функции в точке z.

Если каждому z ставится в соответствие несколько значений 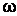, то на области 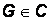задана многозначная функция комплексного переменного.

Например, 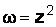– однозначная функция; 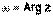– многозначная функция.

Замечание. Так как задание комплексного числа z равносильно заданию двух действительных переменных x и y, то числу 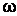тоже соответствуют два действительных числа u и v: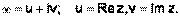

Тогда зависимость 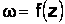равносильна двум зависимостям u = u(x,y), v = v(x,y), т. е.комплексная функция комплексного переменного определяется двумя действительными функциями двух действительных переменных: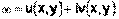

Пример. Найти действительную 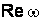и мнимую 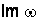части значений функций: а) 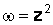; б) .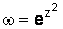

Решение.

а) Запишем комплексное число z в алгебраической форме: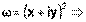

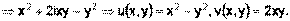
Таким образом .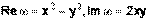

б) Запишем комплексное число z в алгебраической форме:

.

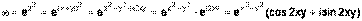Поэтому , .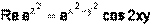

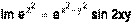Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связываеткомплексную экспоненту с тригонометрическими функциями.

Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство:

,

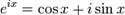где e — основание натурального логарифма,

i — мнимая единица.

При помощи формулы Эйлера можно определить функции sin и cos следующим образом:

,

.

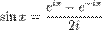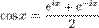Далее можно ввести понятие тригонометрических функций комплексной переменной. Пусть x = iy, тогда:

,

.

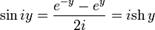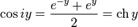Известное тождество Эйлера, связывающее пять фундаментальных математических констант:

e^{i π} + 1 = 0

является частным случаем формулы Эйлера при x = π.

Основна́я теоре́ма а́лгебры утверждает, что

Эквивалентная формулировка теоремы следующая: