Подбор эмпирических формул с помощью метода наименьших квадратов

Пусть мы установим зависимость между двумя величинами х и у.

Будем рассматривать х и у как прямоугольные координаты точек на плоскости. Предположим, что точки с соответствующими координатами почти лежат на некоторой прямой линии. Естественно в этом случае считать, что между х и у существует приближенная линейная зависимость, т.е. что у есть

линейная функция от х, выражающаяся формулой у=ах+b, где а и b- некоторые постоянные коэффициенты. Формулв может быть записана и в другом виде: ах+b-у=0. Т.к. точки х и у только приближенно лежат на прямой, формулы приближенные. Метод наименьших квадратов состоит в том, чтобы подобрать коэффициент а и b так, чтобы сумма квадратов погрешностей была возможно меньше: U=E₁²+E₂²+…+En²(где Е-некоторые числа не равные нулю, погрешности), если эта минимальная сумма квадратов окажется малой, тогда и сама погрешность будет малой по абсолютной величине.

Еi= ах_i+b-у_i, i=1,2,…,n

U= 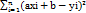x_i и y_i-известные с таблицы числа. A и b- неизвестные.

Таким образом можно рассмотреть функцию двух переменных а и b. Подберем а и b так, чтобы U получило возможно меньшее значение. , . ; ; ;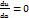

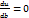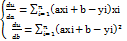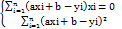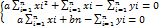6.1. Дифференциальное уравнение n-го порядка. Общее и частное решение. Задача Коши. Краевая задача.

Дифференциальные уравнения называют уравнения, связывающие между собой независимую переменную х, искомую функцию у и ее производные различных порядков по х. порядок старшей производной, входящее в данное дифференциальное уравнение, называется порядком этого уравнения. Таким образом. Общий вид Д.У. n-го порядка следующий: F(x,y,y’,y’’,…y⁽ⁿ⁾)=0

Определение 1: Общим решением дифференциального уравнения называется такое решение его у= (x, C1,C2,…,Cn) которое содержит столько независимых произвольных постоянных C1,C2,…,Cn каков порядок этого уравнения. При этом произвольные постоянные называются независимыми, если общее число постоянных, входящие в состав функции , не может быть уменьшено путем введения других произвольных постоянных, непрерывно зависящих от данных.

Определение 2: всякое решение дифференциального уравнения, которое получается из общего решения, если приписать определенные значения произвольным постоянным, в него входящим, называется частным решением этого дифференциального уравнения.

Задача Коши: найти решение у= 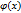дифференциального уравнения, удовлетворяющего заданному начальному условию: у= 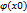, т.е. принимающее при х=х₀ заданное значение у=у₀. Геометрическая задача Коши формируется так: найти интегральную кривую дифференциального уравнения, проходящую через заданную точку М(х₀,у₀).