Определение функции нескольких переменных. Область определения и множество значений. Непрерывность. Частные производные полный дифференциал. Экстремумы

Если в каждой точке М из множества {м}, м-мерного пространство Е^м ставится в соответствии некоторое число u, то говорят что на множестве {м} задана функция u=u(м) или u=f(м). Множество {м} – областью задания функции. Число n соответствующая в данной точке М из множества {м} будем называть частным значением функции в точке М. В совокупности всех частных значений функций или u=f(м) множество значений функций. т.к. точка М определяется м координатами Х₁,Х₂…Х_м, то для функции или u=f(м) м переменных используются также обозначения или u=f(Х₁,Х₂…Х_м).

Замечание: всякая функция от нескольких переменных становится функцией от меньшего числа переменных, если часть переменных зафиксировать, т.е. придать постоянные значения. Например: пусть мы имеем функцию u=f(X, Y, Z). Если предположить, что Z сохраняет постоянное значение Z=c, то мы получим функцию от двух переменных X и Y: u=f(X, Y, с). Далее, предполагая, что две переменные Y и Z сохраняет неизменные значения Y=b, Z=c, то получим функцию u=f(X, b, c)от одной переменной.

Определение 1: если f(x, y) называется непрерывной в точке (x₀, y₀), если: 1) функция определена в данной точке и эта точка является предельной для области существования функции; 2) бесконечно малым приращениям ∆х₀=х-х₀, ∆у₀=у-у₀ переменных х и у соответствует бесконечно малое приращение f(x₀, y₀) функции f(x, y), т.е. при любом способе стремления приращений ∆х₀ и ∆у₀ к нулю, для которых f(х+х₀,у+у₀) имеет смысл, выполнено условие:

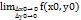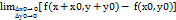= =0.

Определение 2: функция f(x, y) называется непрерывной в данной области, если эта функция непрерывна в каждой точке рассматриваемой области, т.е. если для каждой точки (x, y) области имеем:

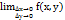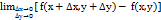= =0, причем здесь мы предполагаем, что смещенная точка 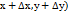принадлежит данной области и 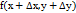существует. Таким образом, можно сказать, что функция непрерывна тогда и только тогда, когда бесконечно малым приращениям ее аргументов соответствует бесконечно малое приращение функции.

Определение: частной производной функции от нескольких переменных по одной из этих переменных называется предел отношений соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при условии, что последнее стремиться к нулю.

Пусть дана функция z=f(x, y), которая определена в некоторой окрестности этой точки. Рассмотрим отношение частного приращения ∆_Хz=f(х + ∆х, у)-f(х, у), функции z по переменной х к приращению ∆х этой переменной: .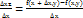

Предел этого отношения при ∆х, стремяшемся к нулю называется частной производной функции z=f(x, y) по х и обозначается так: 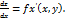Следовательно 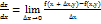. Аналогично определяется частная производная 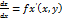от функции х=f(x, y) по у: 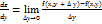. Заметим, что если от функции z=f(x, y) берется производная 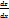, то у считается постоянным; а если же находится 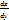, то х считается постоянным.

Определение 1: под дифференциалом независимой переменной понимается приращение этой переменной, т.е. dx=∆x и dy=∆y.

Определение 2: полным дифференциалом функции z=f(x, y) двуз независимых переменных х и у называется главная линейная часть полного приращения этой функции. Dz = A∆x + B∆y. ∆z – dz = 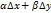, где α, β- бесконечно малые. Функция имеющая данный дифференциал данной области называется дифференцируемой.

Теорема 1: Дифференциал функции равен сумме произведения частных производных этой функции на дифференциалы соответствующих переменных. Док-во: пусть функция z=f(x, y) дифференцируема, т.е. имеет дифференциал Dz = A∆x + B∆y

Для определения коэффициентов А и В напишем полное приращение функции ∆z = A∆x + B∆y +α∆x +β∆y, где α и β-бесконечно малые при ∆х 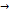0 и ∆у 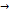0. Полагая ∆у=0 в предыдущей формуле, получим частное приращение ∆_хz = A∆x +α∆x. Отсюда 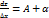. и следовательно при ∆х 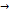0 будем иметь 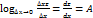. Аналогично, полагая ∆х 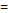0, находим 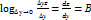. Таким образом, 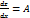, 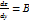. Подставив эти значения в формулу и учитывая, что ∆х=dx и ∆у=dy, получим dz=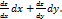

Теореме 2: Достаточное условие дифференцируемости функции. Если функция z=f(x, y) обладает непрерывными частными производным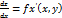и и 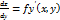в данной области, то эта функция дифференцируема в этой области и ее дифференциал выражается формулой dz= .

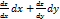Определение: максимумом функции f(x, y) называется такое значение f(x₁, y₁) этой функции, которое больше всех ее значений f(x, y), принимаемых данной функцией в точках некоторой окрестности точки (x₁, y₁). Минимумом функции f(x, y) называется такое значение f(x₂, y₂) этой функции, которое меньше всех ее значений f(x, y), принимаемых данной функцией в точках некоторой окрестности точки (x₂, y₂). Максимум или минимум функции f(x, y)называется экстремумами этой функции, а точка, в которой достигается экстремум, называется точкой экстремума.

Теорема: в точке экстремума функции нескольких переменных каждая ее частная производная первого порядка либо равна нулю, либо не существует. Док-во: рассмотрим функцию двух переменных u=f(x,y) и пусть f(x₀,y₀)- ее максимум. Зафиксируем переменную у, полагая у=у_0. Тогда получим функцию одной переменной u₁=f(x,y₀), которая будет иметь максимум при х=х₀. 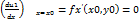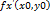От сюда на основании теории экстремума функции одной переменной получаем, что или не существует. 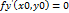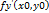Таким же способом доказывается, что или не существует.

Замечание 1: точку, в которой частные производные первого порядка некоторой функции либо равны нулю, либо не существуют, называют критической для этой функции. Тогда теорема эквивалентна утверждению: экстремумы функции нескольких переменных могут достигать лишь в критических точках ее.

Замечание 2: введенные выше условия экстремума функции не являются достаточными, т.е. если, например, в некоторой точке все частные производные первого порядка функции равны нулю, то в этой точке функция не обязательно имеет экстремум.