2015-08-12
621
Линейным дифференциальным уравнением n -го порядка называется уравнение, в которое неизвестная функция y (x)и её производные входят линейно, т.е. в первой степени:
  ;
|
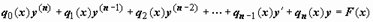Если старший коэффициент q 0 (x) отличен от нуля на интервале (a, b), т.е.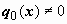 
для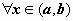 
, то, умножая (19) на 
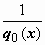, приводим уравнение к виду со старшим коэффициентом, равным 1:
 ;
|
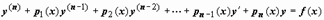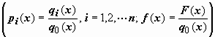; дальше мы будем рассматривать уравнение (20).
Если правая часть уравнения тождественно равна нулю на рассматриваемом интервале (f (x)=0 при 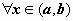), то уравнение называется однородным. Таким образом, однородное уравнение - это уравнение вида
 ;
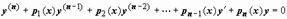| (21) |
Задача Коши для уравнений (20) и (21) ставится также, как и для общего уравнения n -го порядка (17)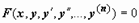 
: требуется найти решение уравнения (20) или (21), удовлетворяющее начальным условиям
|
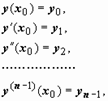
где y 0, y 1, y 2, …, yn -1 - заданные числа. Для уравнения (17) теорема существования и единственности решения задачи Коши требовала непрерывности функции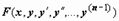 
и её производных 
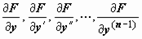; если привести (20) к виду (17):
,
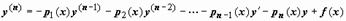то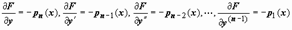 
. Таким образом, условия теоремы Коши приводят к необходимости непрерывности функций f (x) и pi (x), i = 1, 2, …, n. Далее, вывод теоремы Коши для уравнения (17) заключался в том, что найдётся окрестность точки x 0, в которой существует однозначно определённое решение задачи Коши; для линейных уравнений (20) и (21) вывод более глобален: единственное решение существует на всём интервале (a, b), на котором выполняются условия теоремы:
Теорема существования и единственности решения задачи Коши для линейного уравнения: если функции f (x), pi (x), i = 1, 2, …, n непрерывны на интервале (a, b), x 0 - произвольная точка этого интервала, то для любых начальных условий (22) существует единственная функция y (x), определённая на всём интервале (a, b) и удовлетворяющая уравнению (20) и начальным условиям (22).
Всё дальнейшее изложение ведётся в предположении, что условиятеоремы существования и единственности решения задачи Коши выполняются, даже если это не оговаривается специально
|
|
|
Однородные уравнения
Функция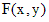 
называется однородной степени 
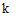, если для всех 
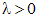выполняется равенство 
.
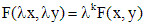Уравнение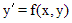 
называется однородным, если правая часть 
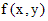является однородной функцией своих аргументов нулевой степени однородности.
Однородные уравнения всегда могут быть представлены в виде
.
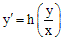Предполагаем, что функция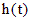 
определена и непрерывна на интервале 
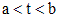и на этом интервале функция 
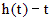не обращается в нуль.
Уравнение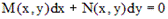 
также является однородным, если 
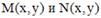однородные функции одной и той же степени однородности.
Однородные уравнения решаются посредством замены переменных:
.
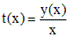Произведя такую подстановку, для новой неизвестной функции t(x) получаем уравнение
|
|
|
.
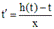Полученное уравнение является уравнением с разделяющимися переменными.
Определение. Уравнение вида
F (x, y, y', y'',…, y ( n )) = 0, (*)
связывающее аргумент х, функцию у (х) и ее производные, называется дифференциальным уравнением n -го порядка.
Определение. Общим решением дифференциального уравнения n -го порядка называется функция у = φ(х, С 1 ,С 2 ,…,Сn), которая зависит от аргумента х и n независимых произвольных постоянных С 1, С 2, …, Сn, обращающая вместе со своими производными у', у'',…, у ( n ) уравнение (*) в тождество.
Определение. Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С 1, С 2, …, Сn определенные числовые значения.
14.2.1. Как следует из определения 14.1.1, обыкновенным дифференциальным уравнением первого порядка называется уравнение
  ;
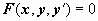| (5) |
где x - независимая переменная, y (x) - неизвестная функция. В форме, разрешённой относительно производной, уравнение первого порядка записывается так:
 ;
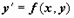| (6) |
Если пользоваться другим обозначением производной, то можно записать (6) как
 ;
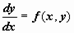| (7) |
Общее решение (общий интеграл) уравнения при n = 1 имеет вид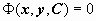 
или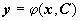 
.
Геометрический смысл уравнения первого порядка. Уравнение (6) в каждой точке (x, y) области D, в которой задана функция f (x, y), определяет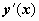 
- угловой коэффициент касательной к решению, проходящему через точку (x, y), т.е. направление, в котором проходит решение через эту точку. Говорят, что уравнение (6) задаёт в D поле направлений. График любого решения дифференциального уравнения (называемый также интегральной кривой) в любой своей точке касается этого поля, т.е. проходит в направлении, определяемом полем. Интегрирование дифференциального уравнения геометрически означает нахождение кривых, у которых направление касательной в каждой точке совпадает с направлением поля. На рисунке справа изображено поле направлений, определяемое уравнением 
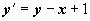, и три интегральные кривые (три частных решения) этого уравнения. Решение можно провести через любую точку области D; единственное решение можно выделить, если задать точку, через которую проходит интегральная кривая:
.
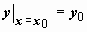Для изображения поля направлений, задаваемого дифференциальным уравнением, рассматривают линии уровня функции f (x, y), т.е. геометрические места точек, в которых касательные к интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами. С помощью изоклин можно приближённо изобразить интегральные кривые.
Для примера построим изоклины уравнения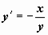 
. Перебираем различные значения постоянной C, строим линии уровня функции 
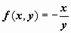, соответствующие этим значениям С (т.е. прямые 
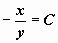), и на этих линиях ставим чёрточки в направлении, определяемым значением С (
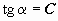, где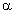 
- угол между чёрточкой и положительным направлением оси Ох): 
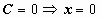- ось Оу; 
; 
; 
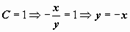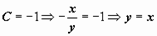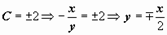и т.д. Информация о направлении интегральных кривых, полученная из рисунка (выше справа), достаточна, чтобы сделать качественный вывод об их поведении: кривые должны огибать начало координат. Это могут быть окружности или спирали (когда мы научимся решать дифференциальные уравнения, мы легко установим, что это окружности; две такие окружности изображены пунктиром).
