Нижче зупинимося лише на основних елементах методики оцінки погрішності інтерполяційних формул, постараючись зберегти її логічну схему.
Нехай y=f(x), - дана функція, а Pn(x)- її інтерполяційний багаточлен. Тоді погрішність Rn(x) інтерполяції функції в точцi х дорівнює
Rn(x)=f(x) – Pn(x),
звідки
f(x)=Pn(x)+Rn(x) (2.8)
Додамо тепер точку x до заданих вузлових точок і розглянемо інтерполяційний багаточлен Pn+1(z) у формі Ньютона, побудований уже по (n+2) точкам х0, х1…хn, x. Його значення в тоці x дорівнює:
Pn+1(x)=f(x)+(x-x0)f(x0, х1)+...+(х-х0)...(х-хn)f(x0,...хn, х)
Але, по побудові, 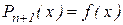 , а перші
, а перші 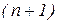 доданків правої частини являють собою
доданків правої частини являють собою 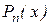 . Таким чином,
. Таким чином,
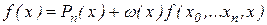 .
.
Порівнюючи тепер це співвідношення з (2.8),одержуємо
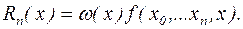 (2.9) (2.9)
|
Це і є одна з форм подання погрішності апроксимації. Її недоліком є та обставина, що для обчислення 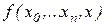 необхідне значення
необхідне значення 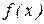 , що невідомо. Як вихід з такого положення залишається взяти лише його наближене значення, тобто
, що невідомо. Як вихід з такого положення залишається взяти лише його наближене значення, тобто 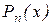 , однак у цьому випадку співвідношення (2.9) стає вже наближеним.
, однак у цьому випадку співвідношення (2.9) стає вже наближеним.
Якщо ж припустити, що функція 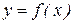 досить гладка й має безперервні похідні до
досить гладка й має безперервні похідні до 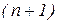 -го порядку включно, то з формули
-го порядку включно, то з формули
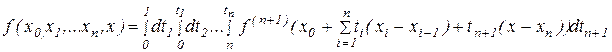 ,
,
справедливість якої треба по індукції, по теоремі про середній випливає співвідношення
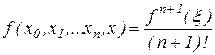 ,
,
де 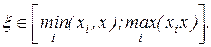 Тоді (2.9) приймає вид
Тоді (2.9) приймає вид
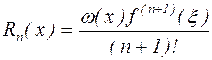 (2.10) (2.10)
|
Недоліком цього співвідношення є те, що невідомо значення 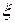 . Однак, якщо відомо вид функції
. Однак, якщо відомо вид функції 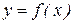 ,те корисної може виявитися оцінка
,те корисної може виявитися оцінка
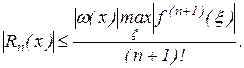
У тому випадку, коли вузлові точки рівновіддалені й 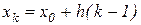 ,
, 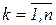 , те по індукції можна показати, що
, те по індукції можна показати, що
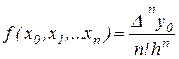 (2.11)
(2.11)
Якщо до них додати точку 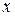 не змінює характер розташування вузлів, то формула залишається справедливої й для розділеної різниці наступного порядку. Т.е.
не змінює характер розташування вузлів, то формула залишається справедливої й для розділеної різниці наступного порядку. Т.е.
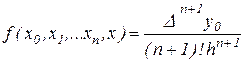 .
.
У противному випадку, остання рівність стає наближеним, і зробивши в 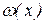 заміну
заміну 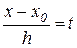 , одержимо
, одержимо 
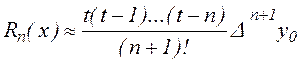 (2.12) (2.12)
|
 2015-08-21
2015-08-21 258
258








