Розглянемо формулу Ньютона (2.7) і припустимо, що вузли є рівновіддаленими, а саме, 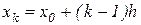 , де
, де 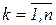 . Зробимо в ній заміну
. Зробимо в ній заміну 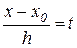 й урахувавши (2.11), одержимо
й урахувавши (2.11), одержимо
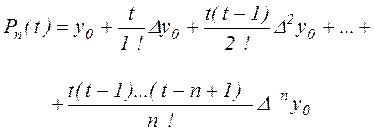 (2.13) (2.13)
|
Це і є багаточлен Ньютона для рівновіддалених вузлів, а погрішність інтерполяції при його використанні оцінюється вираженням (2.12).
Відзначимо, що зі збільшенням порядку значення кінцевої різниці 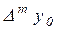 убуває. Тому нерідко необхідна точність обчислення значення функції досягається при меншій кількості доданків, тобто при меншому числі використаних вузлових точок. У зв'язку із цим, залежно від розташування значення x серед масиву значень x0 , x1, … xn на основі (2.7) формують окремі формули, використовувані для інтерполяції на початку, кінці й середині таблиці. Розглянемо ці випадки.
убуває. Тому нерідко необхідна точність обчислення значення функції досягається при меншій кількості доданків, тобто при меншому числі використаних вузлових точок. У зв'язку із цим, залежно від розташування значення x серед масиву значень x0 , x1, … xn на основі (2.7) формують окремі формули, використовувані для інтерполяції на початку, кінці й середині таблиці. Розглянемо ці випадки.
Нехай значення x близько до x0 . Тоді вибираючи для інтерполяції вузлові точки x0 , x0 + h, x0 +m h одержимо
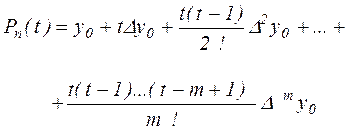 (2.14), (2.14),
|
її погрішність, відповідно до (2.12)
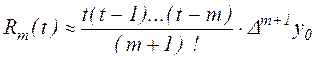
|
Нехай тепер значення x близько до xn, тобто до кінця таблиці. Тоді вибираючи для інтерполяції вузли xn, xn – h,…, xn–mh і зробивши заміну 

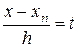 з (2.7) одержуємо
з (2.7) одержуємо
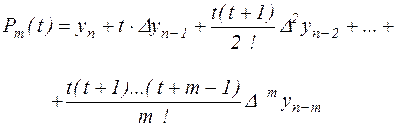 (2.15), (2.15),
|
погрішність інтерполяції
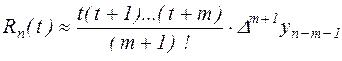 . .
|
Якщо значення x близько до деякому xk , розташованому в середній частині таблиці, то для інтерполяції звичайно використовують точки xk, xk + h, xk -h, …, xk+mh, xk-mh Відповідний інтерполяційний багаточлен також виходить із (2.7) і після заміни 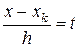 приймаємо
приймаємо
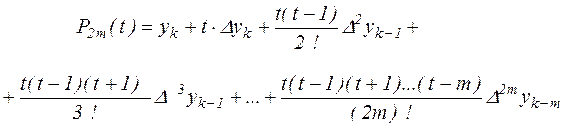 (2.16), (2.16),
|
його погрішність оцінюється вираженням.
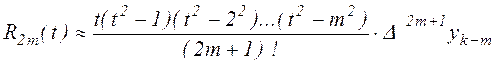 . .
|
Інтерполяційному багаточлену (2.16) можна додати більше симетричний вид. Так, розбиваючи непарні доданки, починаючи із третього, на два, і групуючи з парними, одержимо
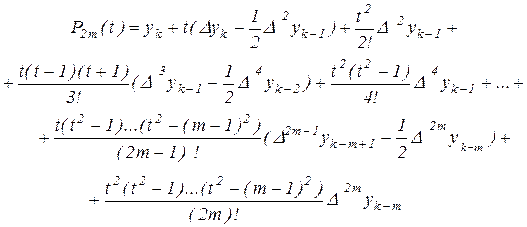
Представимо тепер різниці в дужках у вигляді
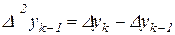 ,
, 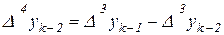 і т.д., одержимо багаточлен,
і т.д., одержимо багаточлен,
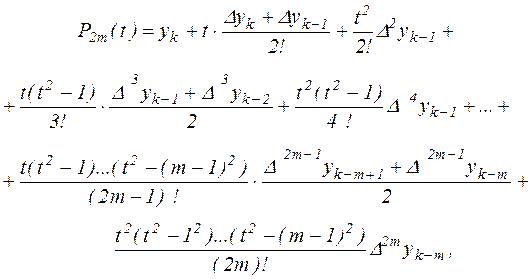
|
який називається інтерполяційним багаточленом Ньютона – Стiрлiнга.
 2015-08-21
2015-08-21 311
311








