2015-08-21
1671
Рассмотрим установившийся поток идеальной жидкости. Как уже говорилось, она не обладает вязкостью, т. е. движется без трения.
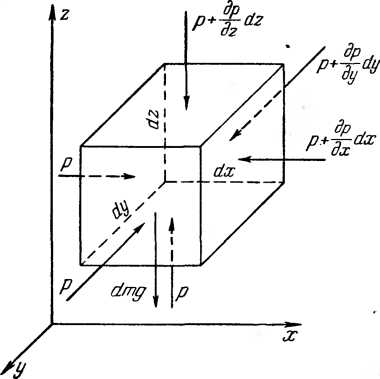
Рис. 7
Выделим в потоке элементарный параллелепипед.объемом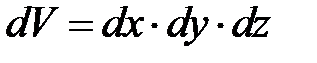 
, ориентированный относительно осей координат (рис. 7).
Проекции на оси координат сил тяжести и давления, действующих на параллелепипед, составляют:
для оси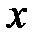 
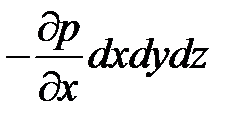
для оси 
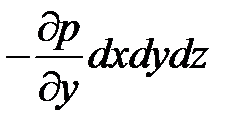
для оси 
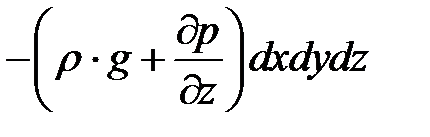
Согласно основному принципу динамики, сумма проекций сил, действующих на движущийся элементарный объем жидкости, равна произведению массы жидкости на ее ускорение.
Масса жидкости в объеме параллелепипеда
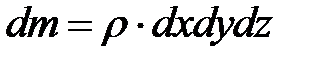
Если жидкость движется со скоростью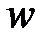 
, то ее ускорение равно 
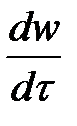, а проекции ускорения на оси координат: 
, 
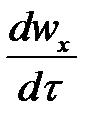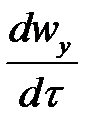и 
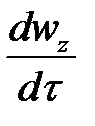, где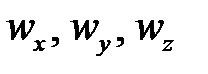 
– составляющие скорости вдоль осей 
.
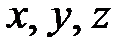В соответствии с основным принципом динамики
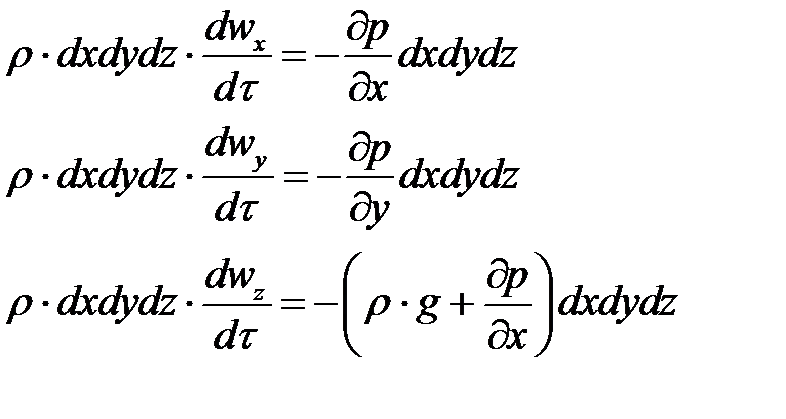
или после сокращения
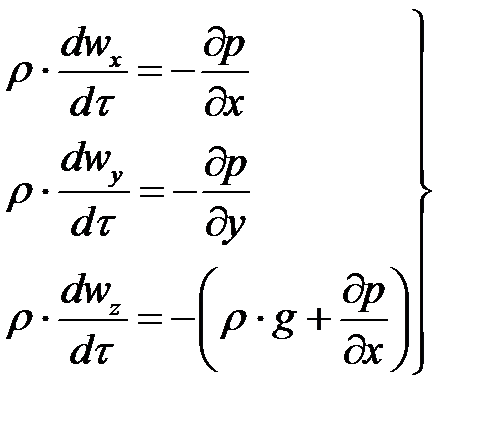 | 4-19 |
Или в другой форме, учитывая что субстанциональные производные соответствующих составляющих скорости равны:
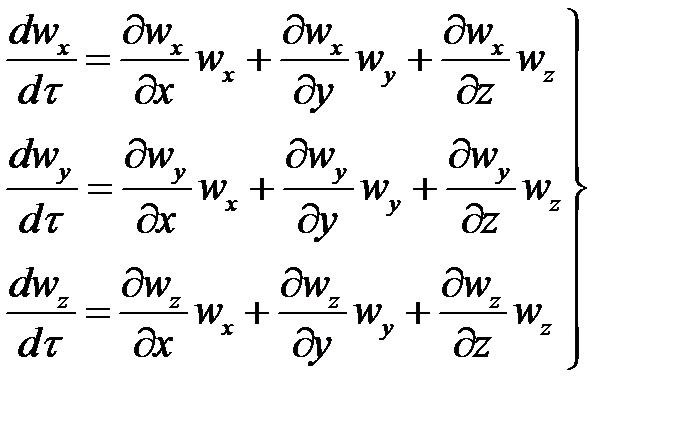 | 4-20 |
Система уравнений (4-19) с учетом выражений (4-20) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для установившегося потока.
