1) выделяются гипотезы Но: 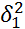 =…=
=…= 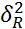 (генеральн. диспесии каждого из ур.=м/у собой)
(генеральн. диспесии каждого из ур.=м/у собой) 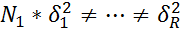
2) несмещен точечные оценки ген. дисперс. ур-ний 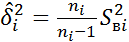 , гдне i=1-R
, гдне i=1-R
3) находится оценка ген диспер. всех ур. 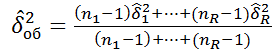
4) находится экспер. знач. параметра 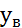 статистики критерия Барл.
статистики критерия Барл. 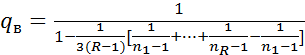
5) Находит эмперич. зн. критерия Бартл. 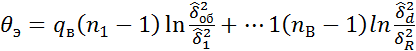
6) определяется кріт зн. статистики критерия Бартл.
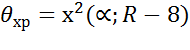 ,
, 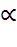 -задан. ур. значимости
-задан. ур. значимости
7) 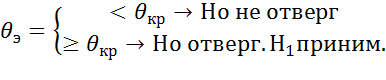
43.Проверка гипотезы о значимости влияния фактора на результативный признак с помощью дисперс анализа.
Значимость фактора на результат признака
Схема проверки:
1) выдвигаются гипотезы Но=влияние фактора на результат не значима, т.е. случ. Н1: значимо, т.е. не случайно.
2) находится ∑результатов наблюдения на каждом из ур. 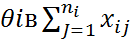
i=1…k
3)находится ∑ результатов не всех ур. вместе 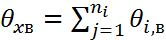
4) Находится ∑ квадратов наблюдений 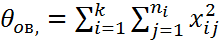
5) Находится ср. знач. ур-нь ∑квадр. 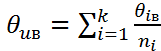
6) находится обяз. ср. ∑ квадратов
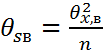 n=n+…+
n=n+…+ 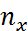
7)находится несмещен. точечная общ. дисперсии всех ур. 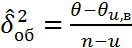
8) -//- несмещ. течечн. оценка ф-рах 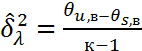
9) экспер. зн. статистики критерия 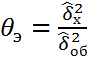
10) опред. крит. зн. статистики критерия 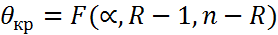 11)
11) 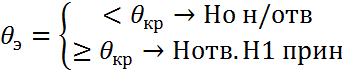
44. Проверка гипотезы о равенстве групповых средних с помощью дисперсионного анализа.
Проверка стат. гипотез с помощью дисперсион. анализа
1)Проверка гипотезы о равенстве ср. значений признака в ГС на всех ур-ях
Схема проверки
1) Формир-е основн и альтерн. ей гипотез Но: х1=х2… = 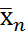 (ген. ср. на всех одинаковы)
(ген. ср. на всех одинаковы)
2) находятся несмещен. течечн. оценки ген. ср. каждого 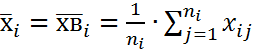 i=1…k
i=1…k
3) находится несмещен. точечная оценка общ. ср. ген зн. всех ур. вместе 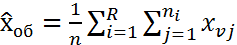
4) Расходится внутригрупповая ∑ квадратов отклонения экспер. данных ур. от уравн. ср. знач-й 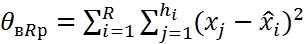
5) 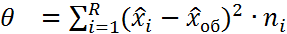
6) находится экспер. зн. статист. критер 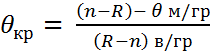
7) находит зн. стат. 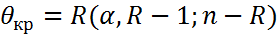
8) 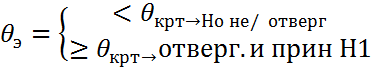
 2015-08-12
2015-08-12 398
398








