Алгебра многочленов
От одной переменной.
Многочлены над полем P.
Пусть 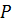 - произвольное числовое поле
- произвольное числовое поле
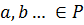
Выражение вида 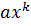 , где
, где 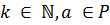 называется одночленом
называется одночленом
Выражение вида 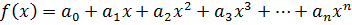 называется многочленом c одной переменной над полем P (обозначается
называется многочленом c одной переменной над полем P (обозначается 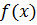 )
)  – коэффициент многочлена,
– коэффициент многочлена, 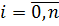
На многочлен можно смотреть как на функцию с областью определения P
Множество всех многочленов обозначается 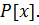
Степенью многочлена  называется наибольший показатель степени переменного. Член, содержащий наибольшую степень называется старшим членом многочлена. Член, не содержащий переменного называется свободным.
называется наибольший показатель степени переменного. Член, содержащий наибольшую степень называется старшим членом многочлена. Член, не содержащий переменного называется свободным.
Теорема. Множество всех многочленов над полем 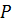 является кольцом
является кольцом
Два многочлена 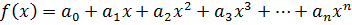 и
и 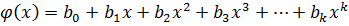 равны, если их соответствующие коэффициенты равны.
равны, если их соответствующие коэффициенты равны.
Суммой двух многочленов  и
и  назовем многочлен
назовем многочлен 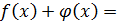
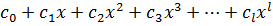 коэффициенты, которого являются суммой соответствующих коэффициентов.
коэффициенты, которого являются суммой соответствующих коэффициентов.
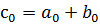
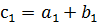
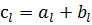
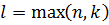 при
при 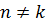
Если 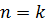 то
то 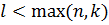 = n
= n
Пример: Сложить 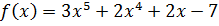
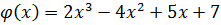
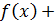
 =
= 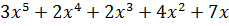
Степень суммы (ст. ( 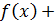
 ) < max(n, k))
) < max(n, k))
Свойства сложения:
1. Сложение многочленов коммутативно
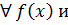

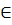
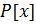
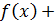
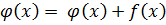 так как сложение многочленов сводится к сложению коэффициентов, т. е. чисел из поля
так как сложение многочленов сводится к сложению коэффициентов, т. е. чисел из поля 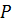
2. Сложение многочленов ассоциативно
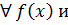

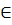
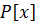 (
( 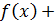
 )+
)+ 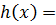
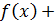 (
(  +
+ 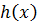 )
)
3. Во множестве всех многочленов существует нулевой многочлен (все коэффициенты которого являются нулями)
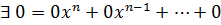
 + 0 =
+ 0 = 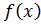
4. 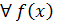
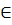
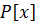
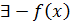
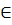
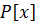
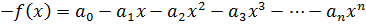
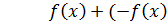 )= 0
)= 0
Вводим операцию умножения
Произведением двух многочленов  и
и  назовем многочлен
назовем многочлен 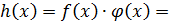
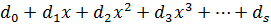
Где: 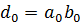
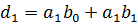
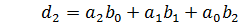
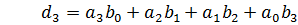
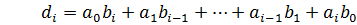
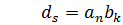
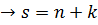
Чтобы перемножить два многочлена нужно каждый член первого умножить на все члены второго и привести подобные слагаемые.
Пример: 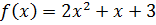
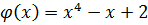
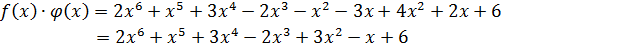
При умножении многочленов старший член произведения равен произведению старших членов. Свободный член произведения равен произведению свободных членов. Степень произведения 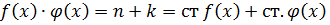 (сумма степеней сомножителей)
(сумма степеней сомножителей)
Произведение двух многочленов равно нулевому многочлену тогда и только тогда, когда хотя бы один из многочленов равен нулевому.
Докажем что умножение многочленов дистрибутивно относительно сложения.
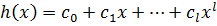
Покажем, что выполняется равенство
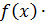 (
( 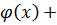
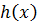 )
) 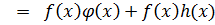
ст. = (n+k) n+k > n+ 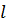
n+k
Покажем, что они имеют одинаковую степень
Пусть для определенности 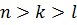 , тогда ст. (
, тогда ст. (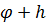 )= k, ст.
)= k, ст. 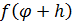 =n+k
=n+k
Докажем равенство коэффициентов
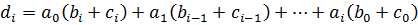
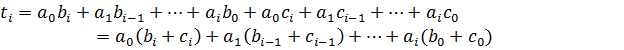
Значит, 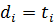 . Так как
. Так как 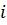 произвольный, то все коэффициенты многочлена стоящие в левой части равны коэффициентам, стоящим в правой части
произвольный, то все коэффициенты многочлена стоящие в левой части равны коэффициентам, стоящим в правой части
Значит 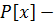 кольцо.
кольцо.
Нетрудно доказать, что умножение многочленов коммутативно и ассоциативно, значит кольцо – коммутативно ассоциативное.
Кольцо содержит единичный элемент 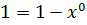
(1 – многочлен нулевой степени)
Теорема. Многочлен 
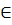
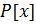 имеет себе обратный тогда и только тогда, когда
имеет себе обратный тогда и только тогда, когда 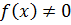 .
.
Пусть 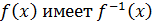 тогда
тогда 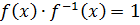
 2015-08-13
2015-08-13 6255
6255







