2015-08-13
4007
В кольце многочленов операция деления не выполнима, однако существуют такие многочлены, что один из них делится на другой.
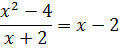
Во множестве всех многочленов вводится понятие делимости.
Говорят многочлен 
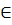
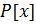делится на 
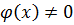, если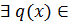 
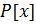, такой что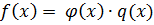 
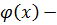делитель , 
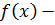кратное 
Свойства делимости многочленов:
1. 
, 
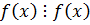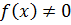
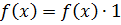
2. 
, 
,
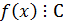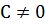
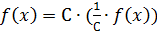
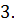
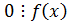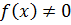
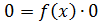
4. 
; 
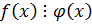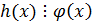, то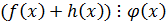 
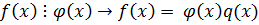
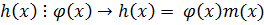
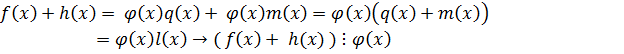
5. Есл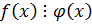и и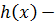 
любой, то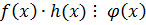 
Свойство 3 и свойство 5 выражают достаточное условие делимости суммы и произведения.
6. Если 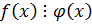а 
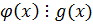, то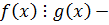 
свойство транзитивности.
7. Если 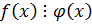, то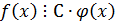 
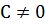
8. Если степени n, то любой делитель многочлена имеющий степень n имеет вид: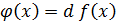 
, 
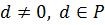
9. и делятся друг на друга тогда и только тогда, когда они отличаются друг от друга числовым множителем.
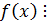
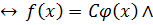
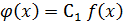
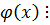
Доказательство:
1)Необходимость.
Дано.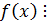 
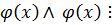
Доказать.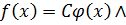 
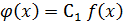
Доказательство.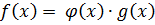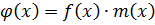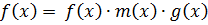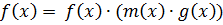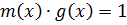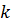
Ст. 
Ст.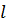 
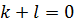
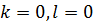
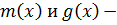многочлены нулевой степени, то есть являются числами из поля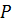 
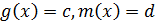, d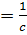 
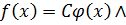
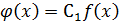
2)Достаточность.
Дано.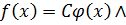 
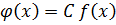
Доказать.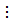 
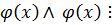
Доказательство. Из условий и определения делимости следует, что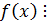 
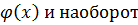
10. Делители многочленов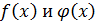 
одни и те же.
