Определение. 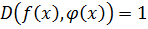 , тогда
, тогда 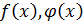 – взаимно-простые.
– взаимно-простые.
Теорема 1 (критерий):
 ,
,  взаимно-простые ó
взаимно-простые ó 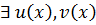 над P
над P 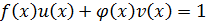 .
.
Доказательство:
1. Необходимость этого условия вытекает из теоремы о линейном представлении НОД.
2. Достаточность.
Дано: 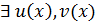
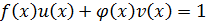
Доказать: 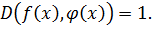
Метод «от противного».
Пусть 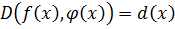
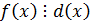
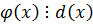
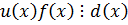
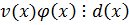
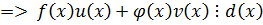
1 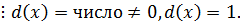
Теорема 2:
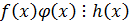 и
и 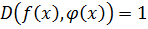 , то
, то 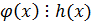 .
.
Доказательство:
Т.к. 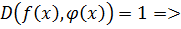 по теореме 1
по теореме 1
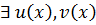
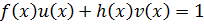 |
| 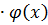
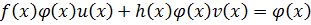
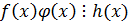 ,
, 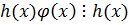
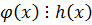 .
.
Теорема 3:
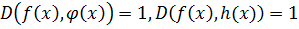 , то
, то
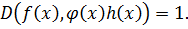
Доказательство:
Из 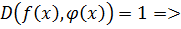 что
что 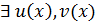 над P
над P
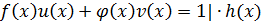
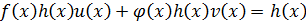
Если бы 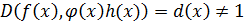 , то
, то
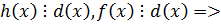 общий делитель
общий делитель 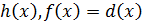 ,
,
а по условию 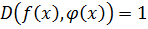 - противоречие =>
- противоречие =>
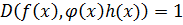 .
.
Теорема 4:
Если 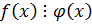 и
и 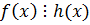 и
и 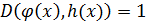 , то
, то 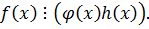
Доказательство:
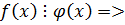
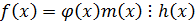 ,
, 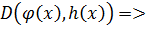
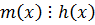
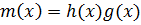
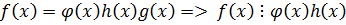 .
.
 2015-08-13
2015-08-13 4807
4807








