Даны 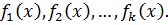
Общим делителем двух или нескольких многочленов над полем 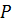 называют многочлен
называют многочлен 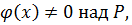 на который делится каждый из данных многочленов
на который делится каждый из данных многочленов 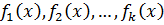 .
.
Множество общих делителей не пустое, так как 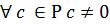 будет общим делителем любых многочленов.
будет общим делителем любых многочленов.
НОД двух или нескольких многочленов называется такой их общий делитель 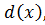 который делится на любой другой их общий делитель
который делится на любой другой их общий делитель 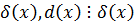 ,
, 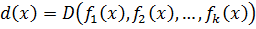 .
.
Существует ли для любых двух многочленов НОД, если существует, то однозначен или нет, как их находить? Ответ на эти вопросы – алгоритм Евклида.
Даны 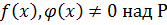 .
.
Сравним степени n и m. Многочлен большей степени делим на многочлен меньшей степени. Если их степени равны, то неважно, какой многочлен, на какой делить. По теореме о делении с остатком 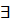
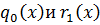 такие, что
такие, что 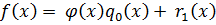 .
.
Если 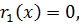 то процесс останавливается.
то процесс останавливается.
Если 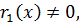 то делим
то делим 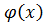 на
на 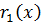 .
.
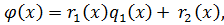 ст.
ст. 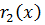 < ст.
< ст. 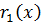 <
< 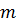
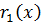 делим на
делим на 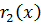
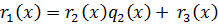 , ст.
, ст. 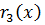 < ст.
< ст. 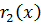 <
< 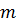
Процесс деления конечен
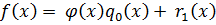
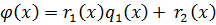
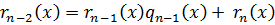
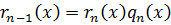
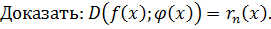
Доказательство: 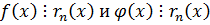
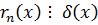 ,
, 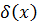 - общий делитель.
- общий делитель.
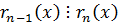 (из последнего)
(из последнего)
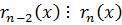 (из предпоследнего)
(из предпоследнего)
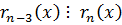 и т. д.
и т. д.
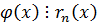
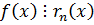 ,
, 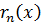 - общий делитель.
- общий делитель.
Покажем, что 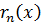 - НОД
- НОД
Пусть 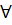
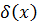 - общий делитель многочленов
- общий делитель многочленов  и
и 
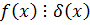
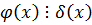
Из (1) 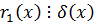
Из (2) 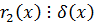
...
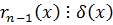
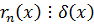
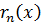 - НОД
- НОД  и
и  .
.
Свойства НОД
1. НОД двух многочленов находится однозначно с точностью до числового множителя. (1)
Доказательство: 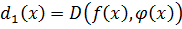
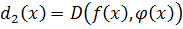
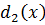 – общий делитель.
– общий делитель.
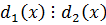
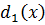 - общий делитель.
- общий делитель.
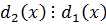
По свойству делимости – два многочлена делятся друг на друга тогда и только тогда, когда они отличаются числовым множителем.
НОД  и
и  среди всех брать тот, у которого старший коэффициент равен 1 (нормированные).
среди всех брать тот, у которого старший коэффициент равен 1 (нормированные).
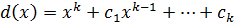
Замечание: Учитывая свойство (1) при нахождении НОД с помощью алгоритма Евклида многочлены  ,
,  ,
, 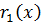 ,
, 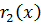 , …,
, …, 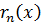 можно заменять другими многочленами, отличными числовыми множителями.
можно заменять другими многочленами, отличными числовыми множителями.
«Теорема о линейном представлении НОД двух многочленов»
Если 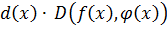 , то
, то 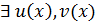
Над P: 1) 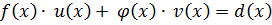
2) ст 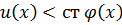
ст 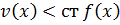
Доказательство:
Доказательство существования 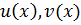 вытекает из алг. Евклида
вытекает из алг. Евклида
из 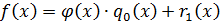 получаем
получаем
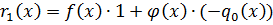
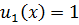 ,
, 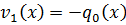
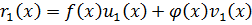
Из 2 равенства: 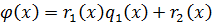
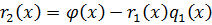
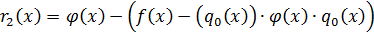
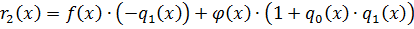
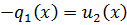 ,
, 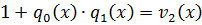
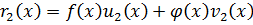 и т.д.
и т.д.
Из предпоследнего: 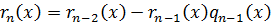
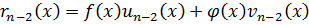
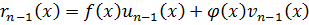
подставим, сгруппируем и получим:
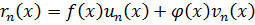
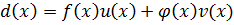
На практике будем находить 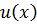 ,
, 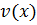 начиная с конца. При этом допускать умножения на числа нельзя.
начиная с конца. При этом допускать умножения на числа нельзя.
Докажем, что ст. 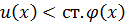
ст. 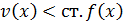
Пусть 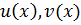 - одна из пар, удовлетворяет теореме
- одна из пар, удовлетворяет теореме
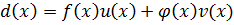 .
.
Пусть ст. 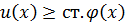 ,
, 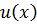 разделим по теореме о делении с остатком
разделим по теореме о делении с остатком  . Найдем часть
. Найдем часть 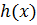 .
.
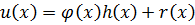
ст. 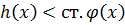
подставим
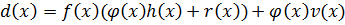
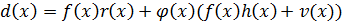
Покажем, что степень многочлена ст. 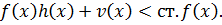
Если бы степень этого многочлена была 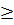 ст.
ст.  , тогда степень пр-я
, тогда степень пр-я  на этот многочлен была бы
на этот многочлен была бы 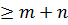 .
.
ст. 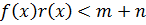
ст. 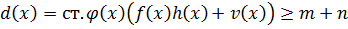 ,
,
d – делитель.
ст. 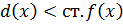
ст. 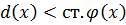
получаем противоречие
ст. 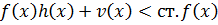
Через 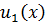 возьмем
возьмем 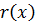 , а через
, а через 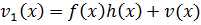 .
.
Получим 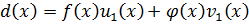 ,
,
где ст. 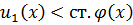 , а ст.
, а ст. 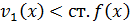 .
.
 2015-08-13
2015-08-13 5218
5218








