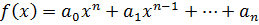 над P.
над P.
Пусть c – любое число из P.
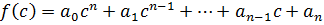 – число из P.
– число из P.
Это число называется значением многочлена  при
при 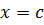 .
.
Пример: 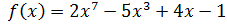
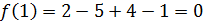
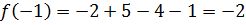
Определение. Число c называется корнем многочлена  , если
, если 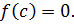
1 – корень многочлена 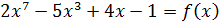 .
.
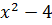 ,
, 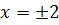 ,
,
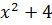 , 2i, -2i,
, 2i, -2i,
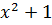 , I, -i.
, I, -i.
Замечание: Если 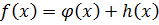 , то
, то 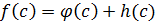 .
.
Деление многочлена на линейный двучлен
ax+b, a≠0
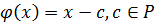
По теореме о делении с остатком:
для 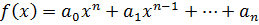 над P найдется
над P найдется 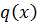 ,
, 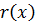
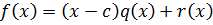
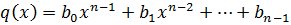
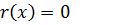 ст.
ст. 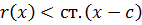
ст. 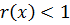
ст. 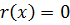 или
или 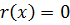
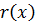 – число из P.
– число из P.
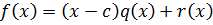
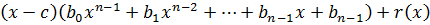
В правой части этого равенства раскроем скобки и сгруппируем по степеням x.
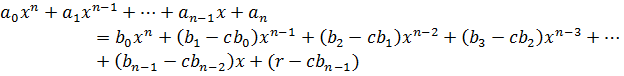
Из равенства многочленов получим равенство их коэффициентов.
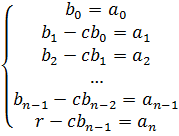
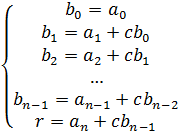
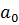 | 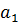 | 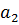 | … | 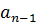 | 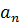 | |
| c | 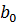 | 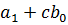 | 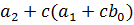 | … | 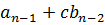 | r= 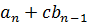 |
Пример:
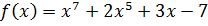
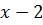
| -7 | ||||||||
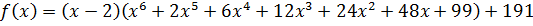
 2015-08-13
2015-08-13 1386
1386








