Алгебраическое определение равенства: (1)
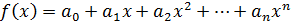
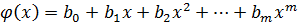
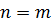
называются равными, если 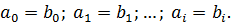
На многочлен  можно смотреть как на функцию: (2)
можно смотреть как на функцию: (2)
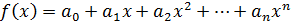
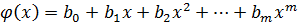
равны (в функциональном смысле), если 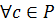 значение
значение 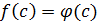 .
.
Теорема:
Алгебраическое и функциональное определения равенства эквивалентны.
Доказательство:
1) Пусть многочлены равны по (1) определению.
Дано: 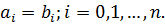
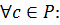
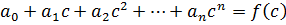
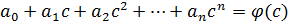
а значение многочлена определено однозначно. Значит 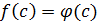 , т.к. коэффициенты равны.
, т.к. коэффициенты равны.
2) Пусть 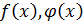 равны по (2) определению.
равны по (2) определению.
Дано: 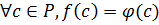
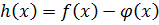
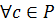 :
: 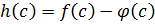
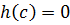
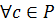 является корнем
является корнем 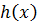 .
.
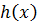 имеет бесконечное множество корней =>
имеет бесконечное множество корней => 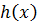 – нулевой многочлен
– нулевой многочлен
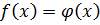
Два множества равны ó их соответствующие коэффициенты равны
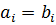 .
.
 2015-08-13
2015-08-13 10455
10455








