2015-08-13
4431
В кольце целых чисел особую роль играют простые числа.
В теории многочленов аналогичную роль играют неприводимые многочлены.
Определение 1: p(x) над P называется неприводимым, если он имеет своими делителями делители вида c и cp(x) и других делителей не имеет.
Определение 2: 
над P называется приводимым, если кроме делителей c и cf(x) этот многочлен имеет другие делители 
, 
.
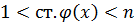R: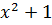 
, 
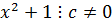
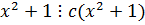
не приводим.
C: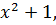 
кроме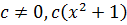 
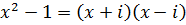
приводимый.
Один и тот же многочлен над одним полем может оказаться неприводим, а над другим приводим.
ст. 
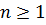называется приводимым над P, если существуют многочлены 
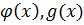над P, что имеет место равенство
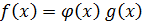
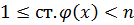
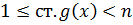
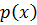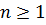ст. называется неприводимым над P, если в любом его представлении вида
(1) 
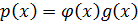
один из многочленов будет иметь 0 степень, другой n.
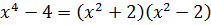
Замечание: Многочлены 0-ой степени играют роль 1. То есть не являются ни приводимыми, ни неприводимыми. Всякий другой многочлен будет либо приводим, либо неприводим.
Свойства:
1. Многочлены 1-ой степени не приводимы над любым числовым полем.
Доказательство:
Дано: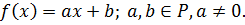 
Пусть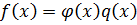 
1 m k
1=m+k ó m=0, k=1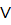 
m=1, k=0
m≥0, k≥0
0-ой степени (число)
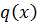- 1-ой степени dx+l
ð неприводим.
2. Если 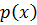неприводим над P, то 
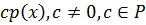тоже неприводим над этим полем.
Доказательство:
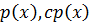по свойству делимости имеют одинаковый делитель, а т.к. 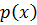имеет делитель 
, 
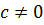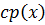те же.
Это свойство позволяет при рассмотрении многочленов приводимых и неприводимых в разложении многочленов на неприводимые множители брать со старшим коэффициентом 1.
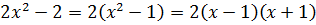
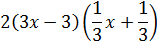
3. Если 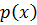неприводим над P, а любой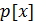 
, то возможны 2 случая:
1) 
;
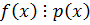2) 
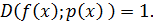
Доказательство:
Рассмотрим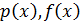 
над P.
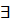НОД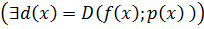 
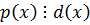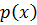, - непр. 
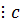и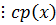 
.
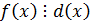
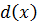- либо число, либо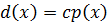 
. 
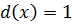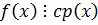
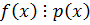
4. Произведение двух или нескольких многочленов ó делится на неприводимый многочлен, когда хотя бы 1 из них 
этот многочлен.
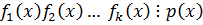ó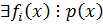 
.
Доказательство:
1. Достаточность следует из свойств делимости.
2. Необходимость для случая 2-х сомножителей:
Дано: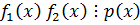 
По предыдущей теореме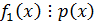 
.
Или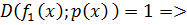 
по теореме о взаимно простых многочленах, то 
.
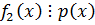Для k-1 сомножителя верна.
Для k сомножителей.
Понятие приводимости многочленов является относительным. Это значит, что один и то же многочлен над одним полем может быть приводим, а над другим нет.
