 с действительными коэффициентами
с действительными коэффициентами
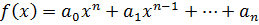 , (1)
, (1)
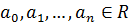 .
.
По основной теореме алгебры этот многочлен имеет хотя бы один комплексный корень (R 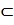 C). Этот корень может быть действительным.
C). Этот корень может быть действительным.
Теорема о сопряженности комплексных корней многочлена с действительными коэффициентами:
Если 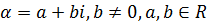 является корнем многочлена (1) с действительными коэффициентами, то число, сопряженное к
является корнем многочлена (1) с действительными коэффициентами, то число, сопряженное к 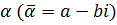 является корнем
является корнем  .
.
Доказательство:
Так как 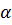 – корень, то
– корень, то 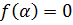 ,
, 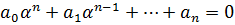 . (2)
. (2)
Из теории комплексных чисел
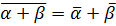 ,
,
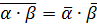 ,
,
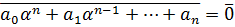 ,
,
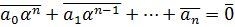 ,
,
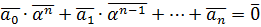 .
.
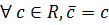 ,
,
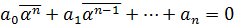 . (3)
. (3)
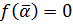 , т.е.
, т.е. 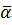 является корнем многочлена. Ч.т.д.
является корнем многочлена. Ч.т.д.
Покажем, что кратность корней 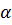 и
и 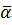 будет одинаковой.
будет одинаковой.
Пусть 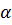 - корень многочлена k -ой кратности,
- корень многочлена k -ой кратности, 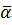 - корень многочлена -ой кратности.
- корень многочлена -ой кратности.
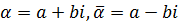 .
.
Учитывая определение кратности
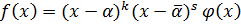 ;
;
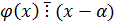 ,
, 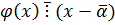 .
.
Надо доказать, что 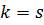 .
.
1) Пусть 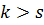 , тогда
, тогда 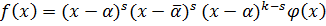 ;
;
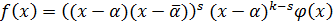 .
.
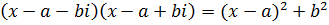 ,
,
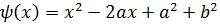 .
.
Получили многочлен второй степени с действительными коэффициентами 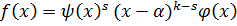 .
.
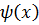 – многочлен с действительными коэффициентами, любая его степень будет многочленом с действительными коэффициентами.
– многочлен с действительными коэффициентами, любая его степень будет многочленом с действительными коэффициентами.
 .к.
.к.  с действительными коэффициентами, ψ
с действительными коэффициентами, ψ 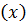 тоже с действительными коэффициентами.
тоже с действительными коэффициентами.
Тогда частное 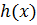 =
= 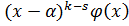 с действительными коэффициентами.
с действительными коэффициентами.
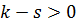 ,
, 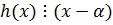 =>
=> 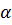 является корнем этого многочлена.
является корнем этого многочлена.
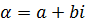 .
.
 .к.
.к. 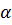 – корень, то
– корень, то 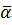 тоже корень
тоже корень 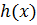 (по предыдущей теореме).
(по предыдущей теореме).
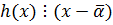 , но
, но 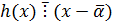 , т.к.
, т.к. 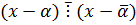 и
и 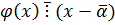 => получили противоречие.
=> получили противоречие.
Предположение, что 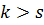 не верно.
не верно.
2) 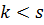 , то аналогично получили бы противоречие.
, то аналогично получили бы противоречие.
=> 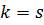 => кратности корней
=> кратности корней 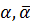 многочлена с действительными коэффициентами одинакова.
многочлена с действительными коэффициентами одинакова.
При этом говорят, комплексные корни многочлена с действительными коэффициентами попарно сопряжены.
Разложение многочлена 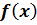 над полем действительных числе на неприводимые множители
над полем действительных числе на неприводимые множители
 с действительными коэффициентами.
с действительными коэффициентами.
Над полем C этот многочлен имеет n корней и разлагается на n линейных множителей.
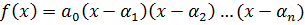 ,
, 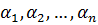 над C.
над C.
Некоторые могут быть действительными.
Пусть для определенности 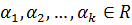
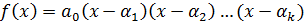 .
.
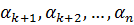 - комплексные корни.
- комплексные корни.
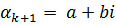 , тогда по теореме о существовании сопряженного корня среди
, тогда по теореме о существовании сопряженного корня среди 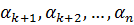 найдется число сопряженное
найдется число сопряженное 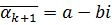 .
.
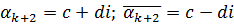 .
.
Комплексных корней четное число и они попарно сопряжены
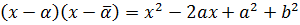 ,
,
с действительными коэффициентами
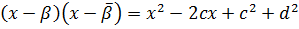 .
.
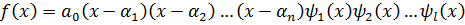 . (*)
. (*)
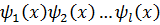 - многочлены второй степени с действительными коэффициентами, корни которых комплексно-сопряженные.
- многочлены второй степени с действительными коэффициентами, корни которых комплексно-сопряженные.
Все множители разложения (*) многочлены с действительными коэффициентами.
Всякий многочлен с действительными коэффициентами над R разлагается на произведение старшего коэффициента, линейных множителей вида 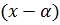 , соответствующих действительным корням, и квадратных множителей
, соответствующих действительным корням, и квадратных множителей 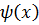 вида
вида 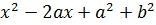 , соответствующих парам комплексно-сопряженных корней.
, соответствующих парам комплексно-сопряженных корней.
Следствие: Неприводимыми многочленами над P являются многочлены 1 степени и 2-ой степени, у которых D<0.
Теорема: Все многочлены выше второй степени над полем действительных чисел приводимы.
Доказательство:
Пусть  с действительными коэффициентами степени
с действительными коэффициентами степени 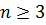 . По основной теореме алгебры существует корень α, если:
. По основной теореме алгебры существует корень α, если:
1) α – действительный корень, 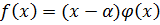 ;
;
2) α - комплексный корень => у многочлена 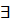
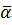
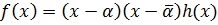 .
.
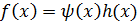 .
.
Все многочлены выше второй степени – приводимы. Ч.т.д.
 2015-08-13
2015-08-13 8178
8178








